% Boyd, "Problems in VLSI design" (Lecture)
% Written for CVX by Almir Mutapcic 02/08/06
%
% We consider the problem of finding optimal width profile
% for a straight wire segmented into N parts. We want to
% minimize the Elmore delay, subject to limits on wire width
% and the total area. We use a pi-model for each wire segment.
% Problem can be formulated as GP:
%
%   minimize   D
%       s.t.   w_min <= w <= w_max
%              area  <= Amax
%
% where variables are widths w (and arrival times T that are used
% to formulate the overall delay D expression).
%
% Important: We label root node as 1, and all the other nodes as
%            node_label_in_the_paper + 1 (due to Matlab's convention).
%            Also label nodes with increasing numbers downstream.

%********************************************************************
% user supplied data (problem constants and tree topology)
%********************************************************************
N = 10+1; % number of segments (including the root node which is labeled as 1)

% parent node array for the straight wire
% specifies which node is a unique parent for node i (always have a tree)
parent = [0:N-1];

% problem constants
Rsource = 0.1;
l = 1*ones(N-1,1);
alpha = 1*ones(N-1,1);
beta  = 1*ones(N-1,1);
gamma = 1*ones(N-1,1);

% load capacitance at each node
Cload = [0; ones(N-1,1)];

% minimum and maximum width and area specification
Wmin = 1;
Wmax = 10;
Amax = 50;

%********************************************************************
% derived data (computed from user's data)
%********************************************************************
% compute children cell array (evaluate who are children for each node)
children = cell(N,1);
leafs = [];
for node = [1:N]
  children{node} = find(parent == node);
  if isempty(children{node})
    leafs(end+1) = node; % leafs have no children
  end
end

%********************************************************************
% optimization
%********************************************************************

disp('Generating the tradeoff curve...')
Darray = []; widths = [];
for Amax = [10.05 10.5 11 12:2:20 22.5 25:5:60]
    fprintf( 'Amax = %5.2f: ', Amax );
    cvx_begin gp quiet
        % optimization variables
        variable w(N-1)     % wire width
        variable T(N)       % arrival time (Elmore delay to node i)

        % objective is the critical Elmore delay
        minimize( max( T(leafs) ) )
        subject to

          % wire segment resistance is inversely proportional to widths
          R = alpha.*l./w;
          R = [Rsource; R];

          % wire segment capacitance is an affine function of widths
          C_bar = beta.*l.*w + gamma.*l;
          C_bar = [0; C_bar];

          % compute common capacitances for each node (C_tilde in GP tutorial)
          C_tilde = cvx( zeros(N,1) );
          for node = [1:N]
            C_tilde(node,1) = Cload(node);
            for k = parent(node)
              if k > 0; C_tilde(node,1) = C_tilde(node,1) + C_bar(k); end;
            end
            for k = children{node}
              C_tilde(node,1) = C_tilde(node,1) + C_bar(k);
            end
          end

          % now compute total downstream capacitances
          C_total = C_tilde;
          for node = N:-1:1
            for k = children{node}
              C_total(node,1) = C_total(node,1) + C_total(k,1);
            end
          end

        % generate Elmore delay constraints
        R(1)*C_total(1) <= T(1,1);
        for node = 2:N
          R(node)*C_total(node) + T(parent(node),1) <= T(node,1);
        end

        % collect all the constraints
        sum(w.*l) <= Amax;
        Wmin <= w <= Wmax;
    cvx_end
    % display and store computed values
    fprintf('delay = %3.2f\n',cvx_optval);
    Darray = [Darray cvx_optval];
    widths = [widths w];
end

% indices of four taper designs on the tradeoff curve
Amax = [10.05 10.5 11 12:2:20 22.5 25:5:60];
A11ind = find(Amax == 11);
A20ind = find(Amax == 20);
A35ind = find(Amax == 35);
A50ind = find(Amax == 50);

% plot the tradeoff curve
figure, clf
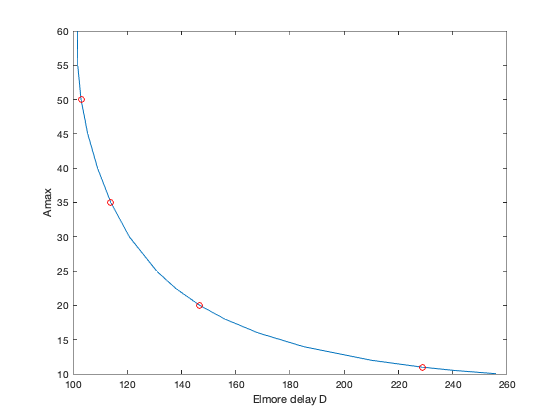
plot(Darray,Amax, ...
     Darray(A11ind),Amax(A11ind),'ro',...
     Darray(A20ind),Amax(A20ind),'ro',...
     Darray(A35ind),Amax(A35ind),'ro',...
     Darray(A50ind),Amax(A50ind),'ro');
xlabel('Elmore delay D'); ylabel('Amax');
disp('Optimal tradeoff curve plotted.')

% plot four taper designs
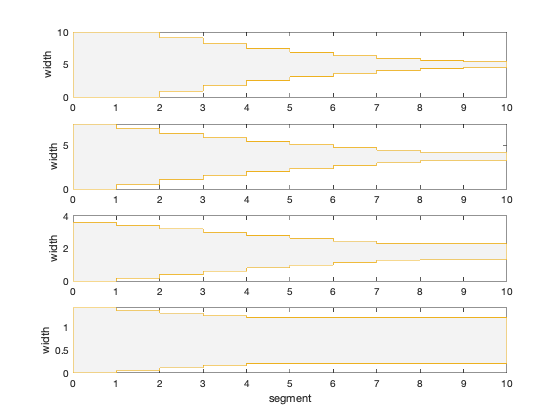
figure, clf
w1 = widths(:,A50ind);
w2 = widths(:,A35ind);
w3 = widths(:,A20ind);
w4 = widths(:,A11ind);
plot_four_tapers(w1,w2,w3,w4);

Generating the tradeoff curve...
Amax = 10.05: delay = 255.72
Amax = 10.50: delay = 241.04
Amax = 11.00: delay = 228.67
Amax = 12.00: delay = 209.98
Amax = 14.00: delay = 184.90
Amax = 16.00: delay = 168.19
Amax = 18.00: delay = 156.01
Amax = 20.00: delay = 146.74
Amax = 22.50: delay = 137.78
Amax = 25.00: delay = 130.82
Amax = 30.00: delay = 120.77
Amax = 35.00: delay = 113.95
Amax = 40.00: delay = 109.06
Amax = 45.00: delay = 105.43
Amax = 50.00: delay = 102.96
Amax = 55.00: delay = 101.76
Amax = 60.00: delay = 101.60
Optimal tradeoff curve plotted.