% Section 5.5,  L. Vandenberghe, S. Boyd, and A. El Gamal
% "Optimizing dominant time constant in RC circuits"
% Original by Lieven Vandenberghe
% Adapted for CVX by Joelle Skaf - 11/27/05
% Modified by Michael Grant - 3/8/06
%
% The problem is to determine the optimal sizes of interconnect wires and
% the optimal distances between them. We will consider an example with 3
% wires, each consisting of 5 segments (see paper, fig.21). The variables
% are the widths wij , and the distances s1 and s2 between the wires.
% The difference with the models used in other scripts is that we include a
% parasitic capacitance between the wires.
% The objective is to minimize the total width s1+s2.
% The problem can be formulated with the following SDP:
%               mimimize    s1 + s2
%                    s.t.   Tmax*G(w11,..,w35)-C(w11,..,w35,t11,..,t23) >=0
%                           1/t1j <= s1 - w1j - 0.5*w2j     , j = 1,..,5
%                           1/t2j <= s2 - w3j - 0.5*w2j     , j = 1,..,5
%                           0 <= tij <= 1         , i = 1,2 , j = 1,..,5
%                           t1 >=0, t2 >= 0, s1 >=smin, s2>=smin
%                           0 <= wij <= wmax
% the 2nd and 3rd constraints are nonlinear convex constraints that can be
% cast as 3 x 3-LMIs (Please refer to the paper for more details).

%
% Circuit parameters
%

n = 6;           % number of nodes per wire
N = 3*n;         % total number of nodes
m = n-1;         % number of segments per wire
alpha = 1;       % conductance per segment is is alpha*size
beta = 0.5;      % capacitance per segment is twice beta*size
gamma = 2;       % coupling capacitance is twice gamma*distance
G0 = 100;        % source conductance
C0 = [10,20,30]; % loads of first, second, third wires
wmin = 0.1;      % minimum width
wmax = 2.0;      % maximum width
smin = 1.0;      % minimum distance between wires
smax = 50;       % upper bound on s1 and s2  (meant to be inactive)

%
% Construct the capacitance and conductance matrices
%   C(x) = C0 + w11 * C1 + w21 * C2 + ...
%   G(x) = G0 + w11 * G1 + w21 * G2 + ...
% and we assemble the coefficient matrices together as follows:
%   CC = [ C0(:) C1(:) C2(:) ... ]
%   GG = [ G0(:) G1(:) G2(:) ... ]
%

CC = zeros(N,N,5*m+1);
GG = zeros(N,N,3*m+1);
for w = 0 : 2,
    % Constant terms
    CC(w*n+n,w*n+n,1) = C0(w+1);
    GG(w*n+1,w*n+1,1) = G0;
    for i = 1 : m,
        % capacitances to ground
        CC(w*n+[i,i+1],w*n+[i,i+1],w*m+i+1) = beta*[1,0;0,1];
        if w < 2,
            % coupling capacitors
            CC(w*n+[i,  n+i  ],w*n+[i,  n+i  ],(w+3)*m+i+1) = gamma*[1,-1;-1,1];
            CC(w*n+[i+1,n+i+1],w*n+[i+1,n+i+1],(w+3)*m+i+1) = gamma*[1,-1;-1,1];
        end
        % segment conductances
        GG(w*n+[i,i+1],w*n+[i,i+1],w*m+i+1) = alpha*[1,-1;-1,1];
    end
end
% Reshape for Matlab use
CC = reshape(CC,N*N,5*m+1);
GG = reshape(GG,N*N,3*m+1);

%
% Compute points the tradeoff curve and the two desired points
%

npts    = 50;
delays  = linspace( 85, 200, npts );
xdelays = [ 130, 90 ];
xnpts   = length(xdelays);
areas   = zeros(1,npts);
xareas  = zeros(1,xnpts);
for j = 1 : npts + xnpts,

    if j > npts,
        xj = j - npts;
        delay = xdelays(xj);
        disp( sprintf( 'Particular solution %d of %d (Tmax = %g)', xj, xnpts, delay ) );
    else,
        delay = delays(j);
        disp( sprintf( 'Point %d of %d on the tradeoff curve (Tmax = %g)', j, npts, delay ) );
    end

    %
    % Construct and solve the convex model
    %

    cvx_begin sdp quiet
        variables w(m,3) t(m,2) s(1,2)
        variable G(N,N) symmetric
        variable C(N,N) symmetric
        minimize( sum(s) )
        subject to
            G == reshape( GG * [ 1 ; w(:) ], N, N );
            C == reshape( CC * [ 1 ; w(:) ; t(:) ], N, N );
            delay * G - C >= 0;
            wmin <= w(:) <= wmax;
            t( : ) <= 1 / smin;
            s( : ) <= smax;
            inv_pos( t(:,1) ) <= s(1) - w(:,1) - 0.5 * w(:,2);
            inv_pos( t(:,2) ) <= s(2) - w(:,3) - 0.5 * w(:,2);
    cvx_end
    ss = cvx_optval;

    if j <= npts,
        areas(j) = ss;
    else,
        xareas(xj) = ss;

        %
        % Draw the wires
        %

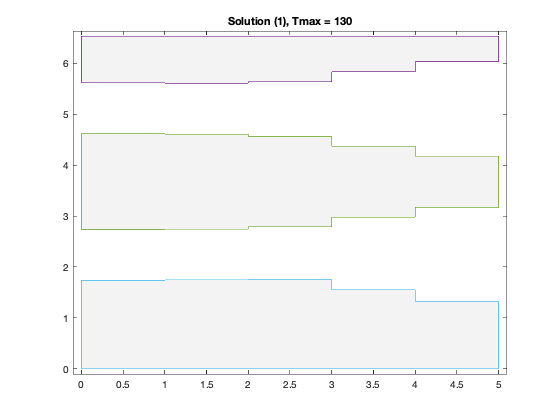
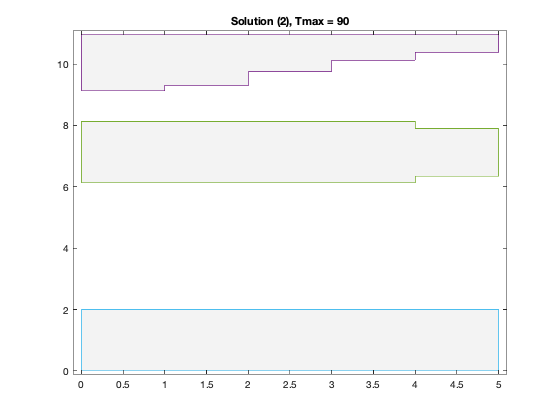
        figure(4*xj-2);
        m2 = 2 * m;
        x1 = reshape( [ 1 : m ; 1 : m ], 1, m2 );
        x2 = x1( 1, end : -1 : 1 );
        y  = [ ss*ones(m2,1), s(2) + 0.5*w(x1,2), zeros(m2,1) ; ...
               ss-w(x2,1),    s(2) - 0.5*w(x2,2), w(x2,3)     ; ...
               ss,            s(2) + 0.5*w(1,2),  0           ];
        x1 = reshape( [ 0 : m - 1 ; 1 : m ], m2, 1 );
        x2 = x1( end : -1 : 1, 1 );
        x  = [ x1 ; x2 ; 0 ];
        hold off;
        fill( x, y, 0.9 * ones(size(y)) );
        hold on
        plot( x, y, '-' );
        axis( [-0.1, m+0.1,-0.1, ss+0.1]);
        colormap(gray);
        caxis([-1,1])
        title(sprintf('Solution (%d), Tmax = %g',xj,delay));

        %
        % Build the state space models and plot step responses
        %

        A = -inv(C)*G;
        T = linspace(0,2*delay,1000);
        B = -A * kron( eye(3), ones(n,1) );
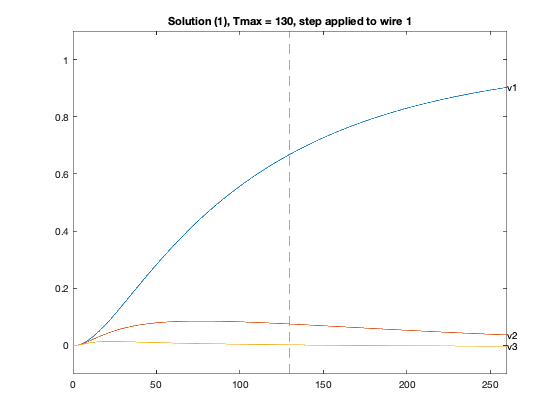
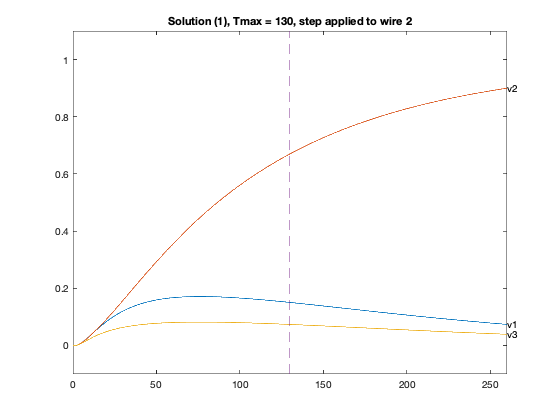
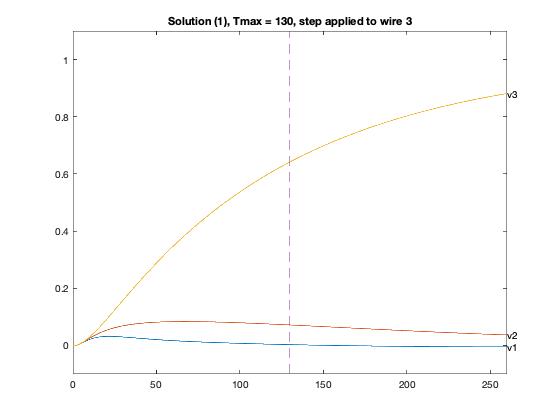
        for inp = 1 : 3,
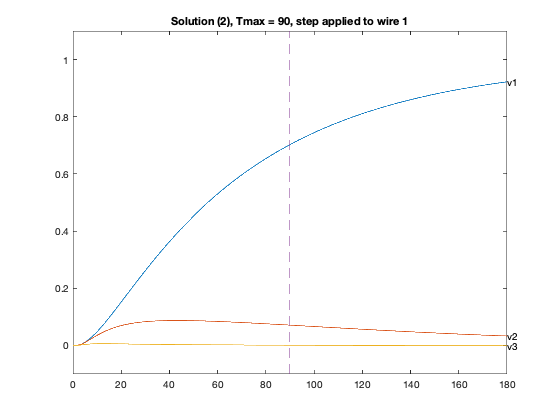
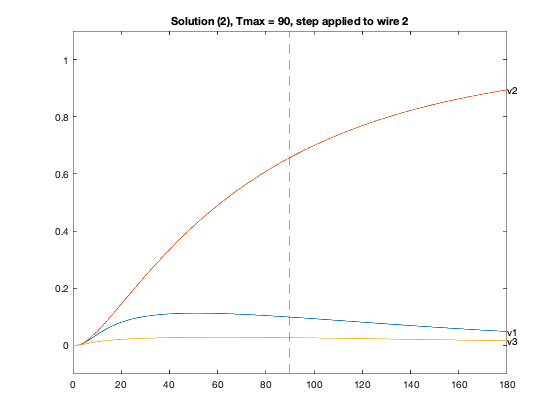
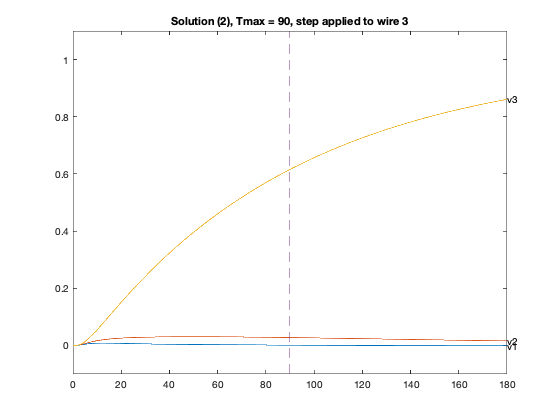
            figure(4*xj-2+inp);
            Y1 = simple_step(A,B(:,inp),T(2),length(T));
            hold off;
            plot(T,Y1([n,2*n,3*n],:),'-');
            hold on;
            text(T(1000),Y1(  n,1000),'v1');
            text(T(1000),Y1(2*n,1000),'v2');
            text(T(1000),Y1(3*n,1000),'v3');
            axis([0 2*delay -0.1 1.1]);
            % show dominant time constant
            plot(delay*[1;1], [-0.1;1.1], '--');
            title(sprintf('Solution (%d), Tmax = %g, step applied to wire %d',xj,delay,inp));
        end

    end

end

%
% Plot the tradeoff curve
%

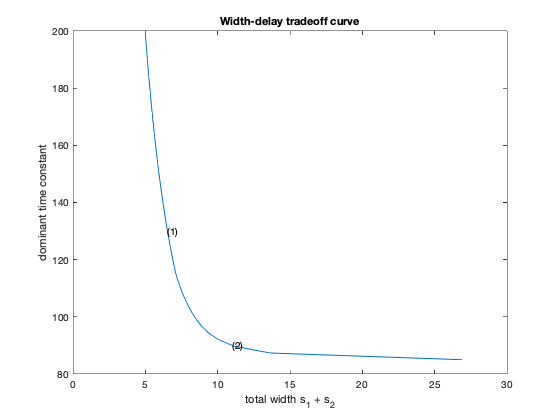
figure(1);
ind = isfinite(areas);
plot(areas(ind), delays(ind));
xlabel('total width s_1 + s_2');
ylabel('dominant time constant');
title('Width-delay tradeoff curve')
hold on;
for k = 1 : xnpts,
    text( xareas(k), xdelays(k), sprintf( '(%d)', k ) );
end

Point 1 of 50 on the tradeoff curve (Tmax = 85)
Point 2 of 50 on the tradeoff curve (Tmax = 87.3469)
Point 3 of 50 on the tradeoff curve (Tmax = 89.6939)
Point 4 of 50 on the tradeoff curve (Tmax = 92.0408)
Point 5 of 50 on the tradeoff curve (Tmax = 94.3878)
Point 6 of 50 on the tradeoff curve (Tmax = 96.7347)
Point 7 of 50 on the tradeoff curve (Tmax = 99.0816)
Point 8 of 50 on the tradeoff curve (Tmax = 101.429)
Point 9 of 50 on the tradeoff curve (Tmax = 103.776)
Point 10 of 50 on the tradeoff curve (Tmax = 106.122)
Point 11 of 50 on the tradeoff curve (Tmax = 108.469)
Point 12 of 50 on the tradeoff curve (Tmax = 110.816)
Point 13 of 50 on the tradeoff curve (Tmax = 113.163)
Point 14 of 50 on the tradeoff curve (Tmax = 115.51)
Point 15 of 50 on the tradeoff curve (Tmax = 117.857)
Point 16 of 50 on the tradeoff curve (Tmax = 120.204)
Point 17 of 50 on the tradeoff curve (Tmax = 122.551)
Point 18 of 50 on the tradeoff curve (Tmax = 124.898)
Point 19 of 50 on the tradeoff curve (Tmax = 127.245)
Point 20 of 50 on the tradeoff curve (Tmax = 129.592)
Point 21 of 50 on the tradeoff curve (Tmax = 131.939)
Point 22 of 50 on the tradeoff curve (Tmax = 134.286)
Point 23 of 50 on the tradeoff curve (Tmax = 136.633)
Point 24 of 50 on the tradeoff curve (Tmax = 138.98)
Point 25 of 50 on the tradeoff curve (Tmax = 141.327)
Point 26 of 50 on the tradeoff curve (Tmax = 143.673)
Point 27 of 50 on the tradeoff curve (Tmax = 146.02)
Point 28 of 50 on the tradeoff curve (Tmax = 148.367)
Point 29 of 50 on the tradeoff curve (Tmax = 150.714)
Point 30 of 50 on the tradeoff curve (Tmax = 153.061)
Point 31 of 50 on the tradeoff curve (Tmax = 155.408)
Point 32 of 50 on the tradeoff curve (Tmax = 157.755)
Point 33 of 50 on the tradeoff curve (Tmax = 160.102)
Point 34 of 50 on the tradeoff curve (Tmax = 162.449)
Point 35 of 50 on the tradeoff curve (Tmax = 164.796)
Point 36 of 50 on the tradeoff curve (Tmax = 167.143)
Point 37 of 50 on the tradeoff curve (Tmax = 169.49)
Point 38 of 50 on the tradeoff curve (Tmax = 171.837)
Point 39 of 50 on the tradeoff curve (Tmax = 174.184)
Point 40 of 50 on the tradeoff curve (Tmax = 176.531)
Point 41 of 50 on the tradeoff curve (Tmax = 178.878)
Point 42 of 50 on the tradeoff curve (Tmax = 181.224)
Point 43 of 50 on the tradeoff curve (Tmax = 183.571)
Point 44 of 50 on the tradeoff curve (Tmax = 185.918)
Point 45 of 50 on the tradeoff curve (Tmax = 188.265)
Point 46 of 50 on the tradeoff curve (Tmax = 190.612)
Point 47 of 50 on the tradeoff curve (Tmax = 192.959)
Point 48 of 50 on the tradeoff curve (Tmax = 195.306)
Point 49 of 50 on the tradeoff curve (Tmax = 197.653)
Point 50 of 50 on the tradeoff curve (Tmax = 200)
Particular solution 1 of 2 (Tmax = 130)
Particular solution 2 of 2 (Tmax = 90)