% Boyd & Vandenberghe "Convex Optimization"
% (a figure is generated)
% Almir Mutapcic 02/08/06
%
% We have a segmented cantilever beam with N segments. Each segment
% has a unit length and variable width and height (rectangular profile).
% The goal is minimize the total volume of the beam, over all segment
% widths w_i and heights h_i, subject to constraints on aspect ratios,
% maximum allowable stress in the material, vertical deflection y, etc.
%
% The problem can be posed as a geometric program (posynomial form)
%     minimize   sum( w_i* h_i)
%         s.t.   w_min <= w_i <= w_max,       for all i = 1,...,N
%                h_min <= h_i <= h_max
%                S_min <= h_i/w_i <= S_max
%                6*i*F/(w_i*h_i^2) <= sigma_max
%                y_1 <= y_max
%
% with variables w_i and h_i (i = 1,...,N).
% For other definitions consult the book.
% (See exercise 4.31 for a non-recursive formulation.)

% optimization variables
N = 8;

% constants
wmin = .1; wmax = 100;
hmin = .1; hmax = 6;
Smin = 1/5; Smax = 5;
sigma_max = 1;
ymax = 10;
E = 1; F = 1;

cvx_begin gp
  % optimization variables
  variables w(N) h(N)

  % setting up variables relations
  % (recursive formulation)
  v = cvx( zeros(N+1,1) );
  y = cvx( zeros(N+1,1) );
  for i = N:-1:1
    fprintf(1,'Building recursive relations for index: %d\n',i);
    v(i) = 12*(i-1/2)*F/(E*w(i)*h(i)^3) + v(i+1);
    y(i) = 6*(i-1/3)*F/(E*w(i)*h(i)^3)  + v(i+1) + y(i+1);
  end

  % objective is the total volume of the beam
  % obj = sum of (widths*heights*lengths) over each section
  % (recall that the length of each segment is set to be 1)
  minimize( w'*h )
  subject to
    % constraint set
    wmin <= w    <= wmax;
    hmin <= h    <= hmax;
    Smin <= h./w <= Smax;
    6*F*[1:N]'./(w.*(h.^2)) <= sigma_max;
    y(1) <= ymax;
cvx_end

% display results
disp('The optimal widths and heights are: ');
w, h
fprintf(1,'The optimal minimum volume of the beam is %3.4f.\n', sum(w.*h))

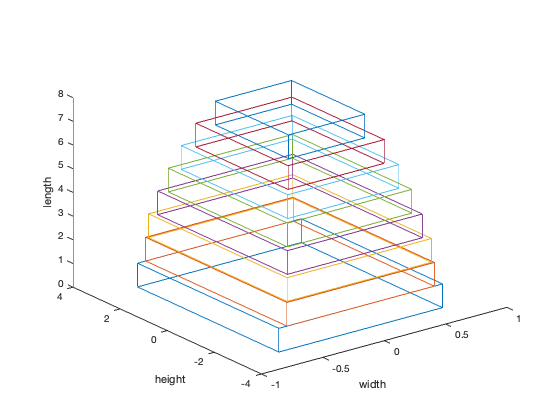
% plot the 3D model of the optimal cantilever beam
figure, clf
cantilever_beam_plot([h; w])

Building recursive relations for index: 8
Building recursive relations for index: 7
Building recursive relations for index: 6
Building recursive relations for index: 5
Building recursive relations for index: 4
Building recursive relations for index: 3
Building recursive relations for index: 2
Building recursive relations for index: 1
 
Calling Mosek 9.1.9: 231 variables, 88 equality constraints
------------------------------------------------------------

MOSEK Version 9.1.9 (Build date: 2019-11-21 11:32:15)
Copyright (c) MOSEK ApS, Denmark. WWW: mosek.com
Platform: MACOSX/64-X86

Problem
  Name                   :                 
  Objective sense        : min             
  Type                   : CONIC (conic optimization problem)
  Constraints            : 88              
  Cones                  : 23              
  Scalar variables       : 231             
  Matrix variables       : 0               
  Integer variables      : 0               

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 8
Eliminator terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries                  : 2                 time                   : 0.00            
Lin. dep.  - tries                  : 1                 time                   : 0.00            
Lin. dep.  - number                 : 0               
Presolve terminated. Time: 0.00    
Problem
  Name                   :                 
  Objective sense        : min             
  Type                   : CONIC (conic optimization problem)
  Constraints            : 88              
  Cones                  : 23              
  Scalar variables       : 231             
  Matrix variables       : 0               
  Integer variables      : 0               

Optimizer  - threads                : 8               
Optimizer  - solved problem         : the primal      
Optimizer  - Constraints            : 33
Optimizer  - Cones                  : 24
Optimizer  - Scalar variables       : 96                conic                  : 71              
Optimizer  - Semi-definite variables: 0                 scalarized             : 0               
Factor     - setup time             : 0.00              dense det. time        : 0.00            
Factor     - ML order time          : 0.00              GP order time          : 0.00            
Factor     - nonzeros before factor : 227               after factor           : 280             
Factor     - dense dim.             : 0                 flops                  : 4.10e+03        
ITE PFEAS    DFEAS    GFEAS    PRSTATUS   POBJ              DOBJ              MU       TIME  
0   1.8e+01  1.3e+00  2.0e+01  0.00e+00   0.000000000e+00   -1.851734604e+01  1.0e+00  0.00  
1   9.3e+00  6.5e-01  8.5e+00  3.63e-02   1.868176734e+00   -1.008757845e+01  5.0e-01  0.01  
2   1.5e+00  1.0e-01  5.2e-01  5.88e-01   4.634902605e+00   2.475911429e+00   7.9e-02  0.01  
3   5.7e-01  4.0e-02  1.1e-01  1.21e+00   4.536227266e+00   3.782997431e+00   3.1e-02  0.01  
4   1.5e-01  1.0e-02  1.5e-02  1.25e+00   3.888521497e+00   3.717150604e+00   8.1e-03  0.01  
5   4.1e-02  2.9e-03  2.1e-03  1.09e+00   3.780646559e+00   3.735536302e+00   2.2e-03  0.01  
6   6.4e-03  4.5e-04  1.4e-04  1.02e+00   3.748436896e+00   3.741401146e+00   3.5e-04  0.01  
7   9.6e-04  6.7e-05  8.0e-06  9.82e-01   3.747590362e+00   3.746525115e+00   5.2e-05  0.01  
8   8.9e-05  6.2e-06  2.2e-07  9.98e-01   3.747129136e+00   3.747030645e+00   4.8e-06  0.01  
9   8.0e-06  5.7e-07  6.1e-09  1.00e+00   3.747072559e+00   3.747063615e+00   4.4e-07  0.01  
10  3.8e-07  2.6e-08  6.2e-11  1.00e+00   3.747067173e+00   3.747066755e+00   2.0e-08  0.01  
11  4.1e-08  2.8e-09  2.2e-12  1.00e+00   3.747066938e+00   3.747066893e+00   2.2e-09  0.01  
Optimizer terminated. Time: 0.02    


Interior-point solution summary
  Problem status  : PRIMAL_AND_DUAL_FEASIBLE
  Solution status : OPTIMAL
  Primal.  obj: 3.7470669382e+00    nrm: 1e+01    Viol.  con: 5e-08    var: 1e-08    cones: 0e+00  
  Dual.    obj: 3.7470668932e+00    nrm: 1e+00    Viol.  con: 0e+00    var: 2e-09    cones: 0e+00  
Optimizer summary
  Optimizer                 -                        time: 0.02    
    Interior-point          - iterations : 11        time: 0.01    
      Basis identification  -                        time: 0.00    
        Primal              - iterations : 0         time: 0.00    
        Dual                - iterations : 0         time: 0.00    
        Clean primal        - iterations : 0         time: 0.00    
        Clean dual          - iterations : 0         time: 0.00    
    Simplex                 -                        time: 0.00    
      Primal simplex        - iterations : 0         time: 0.00    
      Dual simplex          - iterations : 0         time: 0.00    
    Mixed integer           - relaxations: 0         time: 0.00    

------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +42.3965
 
The optimal widths and heights are: 

w =

    0.6214
    0.7830
    0.9060
    1.0124
    1.1004
    1.1762
    1.2000
    1.3333


h =

    3.1072
    3.9149
    4.5299
    5.0620
    5.5018
    5.8811
    6.0000
    6.0000

The optimal minimum volume of the beam is 42.3965.