% Section 8.6.2, Boyd & Vandenberghe "Convex Optimization"
% Original by Lieven Vandenberghe
% Adapted for CVX by Joelle Skaf - 10/16/05
% (a figure is generated)
%
% The goal is to find an ellipsoid that contains all the points
% x_1,...,x_N but none of the points y_1,...,y_M. The equation of the
% ellipsoidal surface is: z'*P*z + q'*z + r =0
% P, q and r can be obtained by solving the SDP feasibility problem:
%           minimize    0
%               s.t.    x_i'*P*x_i + q'*x_i + r >=  1   for i = 1,...,N
%                       y_i'*P*y_i + q'*y_i + r <= -1   for i = 1,...,M
%                       P <= -I

% data generation
n = 2;
rand('state',0);  randn('state',0);
N=50;
X = randn(2,N);  X = X*diag(0.99*rand(1,N)./sqrt(sum(X.^2)));
Y = randn(2,N);  Y = Y*diag((1.02+rand(1,N))./sqrt(sum(Y.^2)));
T = [1 -1; 2 1];  X = T*X;  Y = T*Y;

% Solution via CVX
fprintf(1,'Find the optimal ellipsoid that seperates the 2 classes...');

cvx_begin sdp
    variable P(n,n) symmetric
    variables q(n) r(1)
    P <= -eye(n);
    sum((X'*P).*X',2) + X'*q + r >= +1;
    sum((Y'*P).*Y',2) + Y'*q + r <= -1;
cvx_end

fprintf(1,'Done! \n');

% Displaying results
r = -r; P = -P; q = -q;
c = 0.25*q'*inv(P)*q - r;
xc = -0.5*inv(P)*q;
nopts = 1000;
angles = linspace(0,2*pi,nopts);
ell = inv(sqrtm(P/c))*[cos(angles); sin(angles)] + repmat(xc,1,nopts);
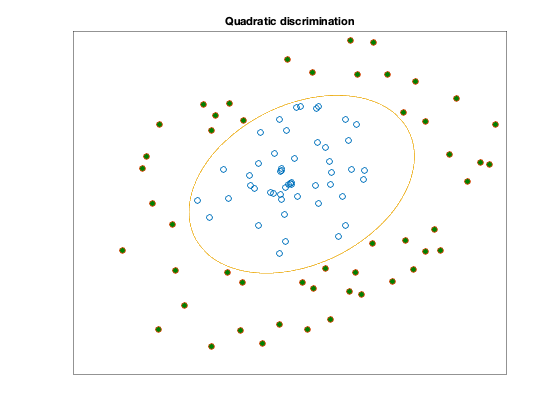
graph=plot(X(1,:),X(2,:),'o', Y(1,:), Y(2,:),'o', ell(1,:), ell(2,:),'-');
set(graph(2),'MarkerFaceColor',[0 0.5 0]);
set(gca,'XTick',[]); set(gca,'YTick',[]);
title('Quadratic discrimination');
% print -deps ellips.eps

Find the optimal ellipsoid that seperates the 2 classes... 
Calling Mosek 9.1.9: 103 variables, 6 equality constraints
   For improved efficiency, Mosek is solving the dual problem.
------------------------------------------------------------

MOSEK Version 9.1.9 (Build date: 2019-11-21 11:32:15)
Copyright (c) MOSEK ApS, Denmark. WWW: mosek.com
Platform: MACOSX/64-X86

Problem
  Name                   :                 
  Objective sense        : min             
  Type                   : CONIC (conic optimization problem)
  Constraints            : 6               
  Cones                  : 1               
  Scalar variables       : 103             
  Matrix variables       : 0               
  Integer variables      : 0               

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries                  : 1                 time                   : 0.00            
Lin. dep.  - tries                  : 1                 time                   : 0.00            
Lin. dep.  - number                 : 0               
Presolve terminated. Time: 0.00    
Problem
  Name                   :                 
  Objective sense        : min             
  Type                   : CONIC (conic optimization problem)
  Constraints            : 6               
  Cones                  : 1               
  Scalar variables       : 103             
  Matrix variables       : 0               
  Integer variables      : 0               

Optimizer  - threads                : 8               
Optimizer  - solved problem         : the primal      
Optimizer  - Constraints            : 6
Optimizer  - Cones                  : 1
Optimizer  - Scalar variables       : 103               conic                  : 3               
Optimizer  - Semi-definite variables: 0                 scalarized             : 0               
Factor     - setup time             : 0.00              dense det. time        : 0.00            
Factor     - ML order time          : 0.00              GP order time          : 0.00            
Factor     - nonzeros before factor : 21                after factor           : 21              
Factor     - dense dim.             : 0                 flops                  : 4.32e+03        
ITE PFEAS    DFEAS    GFEAS    PRSTATUS   POBJ              DOBJ              MU       TIME  
0   1.0e+00  1.8e+01  1.0e+00  0.00e+00   0.000000000e+00   0.000000000e+00   1.0e+00  0.00  
1   4.6e-01  8.5e+00  3.2e+00  -2.73e+00  -3.831728009e+01  0.000000000e+00   4.6e-01  0.01  
2   2.1e-01  3.9e+00  1.1e+00  -6.86e+00  -2.445654132e+01  0.000000000e+00   2.1e-01  0.01  
3   8.4e-02  1.5e+00  4.7e-01  -4.54e-01  -3.091392625e+01  0.000000000e+00   8.4e-02  0.01  
4   7.9e-03  1.5e-01  2.8e-02  1.05e-01   -1.288518935e+01  0.000000000e+00   7.9e-03  0.01  
5   7.5e-05  1.4e-03  3.1e-05  8.76e-01   -1.665478444e-01  0.000000000e+00   7.5e-05  0.01  
6   1.5e-07  2.7e-06  2.6e-09  9.99e-01   -3.255917140e-04  0.000000000e+00   1.5e-07  0.01  
7   2.6e-13  4.9e-12  4.8e-15  1.00e+00   -9.535103919e-10  0.000000000e+00   2.6e-13  0.01  
Optimizer terminated. Time: 0.01    


Interior-point solution summary
  Problem status  : PRIMAL_AND_DUAL_FEASIBLE
  Solution status : OPTIMAL
  Primal.  obj: -9.5351039188e-10   nrm: 3e-10    Viol.  con: 3e-12    var: 3e-12    cones: 0e+00  
  Dual.    obj: 0.0000000000e+00    nrm: 3e+01    Viol.  con: 0e+00    var: 5e-11    cones: 0e+00  
Optimizer summary
  Optimizer                 -                        time: 0.01    
    Interior-point          - iterations : 7         time: 0.01    
      Basis identification  -                        time: 0.00    
        Primal              - iterations : 0         time: 0.00    
        Dual                - iterations : 0         time: 0.00    
        Clean primal        - iterations : 0         time: 0.00    
        Clean dual          - iterations : 0         time: 0.00    
    Simplex                 -                        time: 0.00    
      Primal simplex        - iterations : 0         time: 0.00    
      Dual simplex          - iterations : 0         time: 0.00    
    Mixed integer           - relaxations: 0         time: 0.00    

------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +9.5351e-10
 
Done!