% "Filter design" lecture notes (EE364) by S. Boyd
% (figures are generated)
%
% Designs a frequency-domain and time-domain FIR equalizer for
% a single-input single-output (SISO) channel.
%
% Frequency-domain equalization uses a Chebychev criteria and
% is specified in terms of frequency response functions.
% It is a convex problem (which can be formulated as an SOCP):
%
%   minimize   max |G(w)H(w) - G_des(w)|     for w in [0,pi]
%
% where H is the frequency response function and our variable
% is the filter impulse response h. Function G is the unequalized
% frequency response and G_des is the desired freq response.
%
% Time-domain equalization immediately designs the impulse
% response function by specifying the problem in time (it's an LP):
%
%   minimize   max_{t neq D} |g_tilde(t)|
%       s.t.   g_tilde(D) = 1
%
% where g_tilde is the impulse response of equalized system,
% and D is the delay of the system.
%
% Written for CVX by Almir Mutapcic 02/02/06

%********************************************************************
% problem specs
%********************************************************************
% sample channel with impulse response g
g =.5*[ 0.6526;  0.2157; -0.2639;  1.8024; -0.6430; ...
        0.1096; -0.7190;  0.4206; -0.0193;  0.6603;];

% problem parameters
n  = 30;              % filter order
D  = 10;              % overall delay

%********************************************************************
% frequency domain equalization
%********************************************************************
% number of freq samples (rule-of-thumb)
m  = 15*(length(g) + n);

w = linspace(0,pi,m)';
G = exp( -j*kron(w,[0:length(g)-1]) )*g;
A = exp( -j*kron(w,[0:n-1]) );

% desired frequency response is a pure delay (equalized channel)
Gdes = exp(-j*D*w);

% formulate and solve the Chebyshev design problem
cvx_begin
  variable hf(n,1)
  minimize( max( abs( G.*(A*hf) - Gdes ) ) )
cvx_end

% check if problem was successfully solved
disp(['Frequency equalization problem is ' cvx_status])
if ~strfind(cvx_status,'Solved')
  return
end

%********************************************************************
% time-domain equalization
%********************************************************************
% define the convolution matrix
Tconv = toeplitz([g; zeros(n-1,1)],[g(1) zeros(1,n-1)]);

% create array of all times without t=D
times_not_D = [1:D D+2:size(Tconv,1)];

% formulate and solve the time equalization problem
cvx_begin
  variable t
  variable ht(n,1)

  minimize( max( abs( Tconv(times_not_D,:)*ht ) ) )
  subject to
    Tconv(D+1,:)*ht == 1;
cvx_end

% check if problem was successfully solved
if ~strfind(cvx_status,'Solved')
  disp(['Frequency equalization problem is ' cvx_status])
  return
end

%********************************************************************
% equalizer plots
%********************************************************************
% plot g
figure(1)
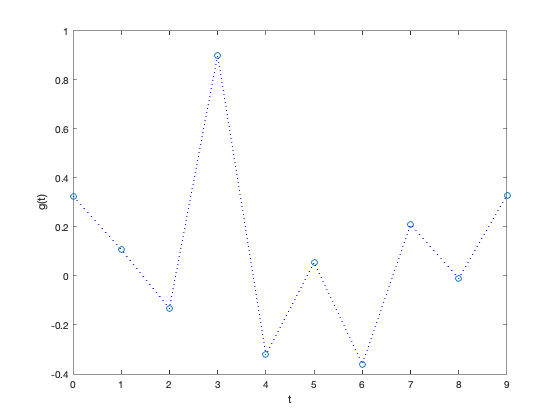
plot([0:length(g)-1],g,'o',[0:length(g)-1],g,'b:')
xlabel('t')
ylabel('g(t)')

figure(2)
H = exp(-j*kron(w,[0:length(g)-1]))*g;
% magnitude
subplot(2,1,1);
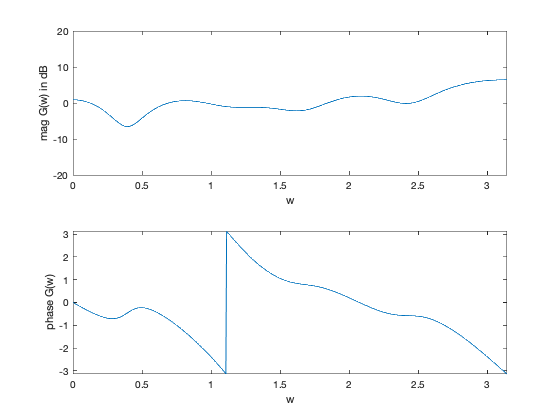
plot(w,20*log10(abs(H)))
axis([0,pi,-20,20])
xlabel('w')
ylabel('mag G(w) in dB')
% phase
subplot(2,1,2)
plot(w,angle(H))
axis([0,pi,-pi,pi])
xlabel('w')
ylabel('phase G(w)')

% freq equalizer
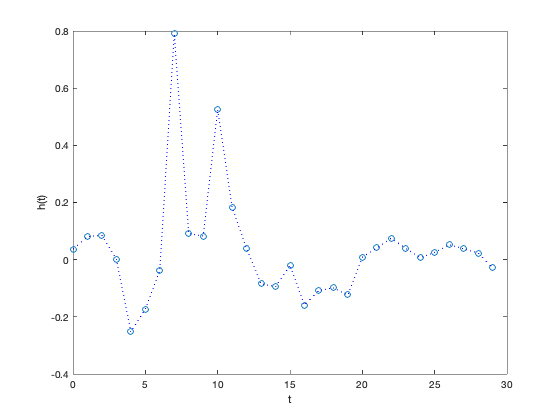
figure(3)
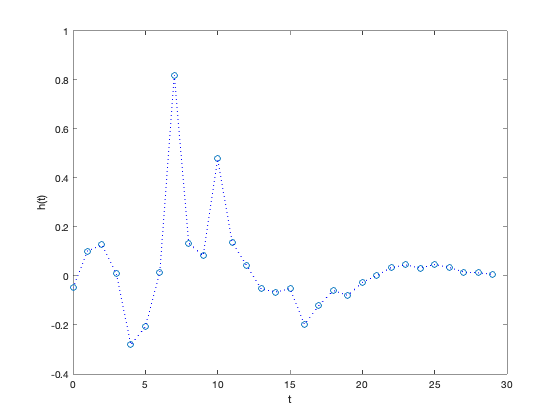
plot([0:n-1],hf,'o',[0:n-1],hf,'b:')
xlabel('t')
ylabel('h(t)')

% plot g_tilde
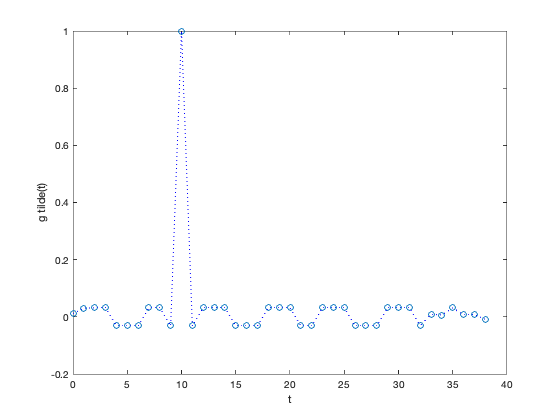
figure(4)
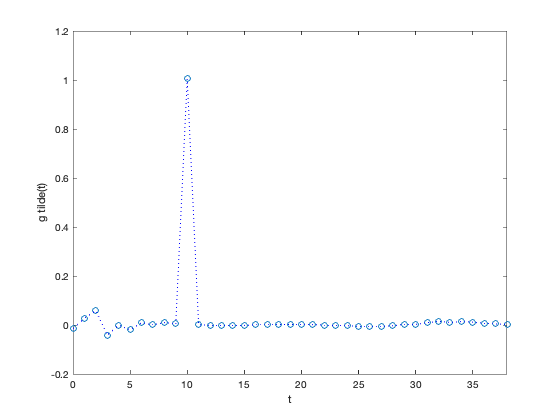
gt=conv(g,hf);
plot([1:length(gt)]-1,gt,'o',[1:length(gt)]-1,gt,'b:')
xlabel('t')
ylabel('g tilde(t)')
axis([0,length(gt)-1,-.2 1.2])

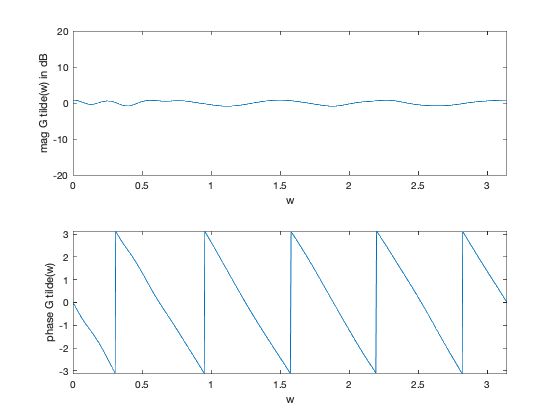
figure(5)
H = exp(-j*kron(w,[0:length(gt)-1]))*gt;
% amplitude
subplot(2,1,1)
plot(w,20*log10(abs(H)))
axis([0,pi,-20,20])
xlabel('w')
ylabel('mag G tilde(w) in dB')
% phase
subplot(2,1,2)
plot(w,angle(H))
axis([0,pi,-pi,pi])
xlabel('w')
ylabel('phase G tilde(w)')

% time equalizer
figure(6)
plot([0:n-1],ht,'o',[0:n-1],ht,'b:')
xlabel('t')
ylabel('h(t)')

% plot g_tilde
figure(7)
gt=conv(g,ht);
plot([1:length(gt)]-1,gt,'o',[1:length(gt)]-1,gt,'b:')
xlabel('t')
ylabel('g tilde(t)')

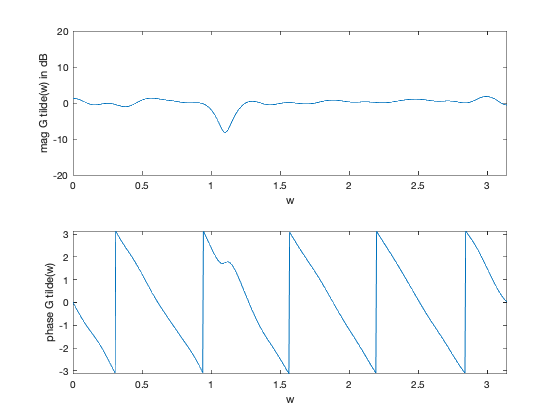
figure(8)
H = exp(-j*kron(w,[0:length(gt)-1]))*gt;
% magnitude
subplot(2,1,1)
plot(w,20*log10(abs(H)))
axis([0,pi,-20,20])
xlabel('w')
ylabel('mag G tilde(w) in dB')
% phase
subplot(2,1,2)
plot(w,angle(H))
axis([0,pi,-pi,pi])
xlabel('w')
ylabel('phase G tilde(w)')

 
Calling Mosek 9.1.9: 2399 variables, 631 equality constraints
   For improved efficiency, Mosek is solving the dual problem.
------------------------------------------------------------

MOSEK Version 9.1.9 (Build date: 2019-11-21 11:32:15)
Copyright (c) MOSEK ApS, Denmark. WWW: mosek.com
Platform: MACOSX/64-X86

MOSEK warning 710: #15 (nearly) zero elements are specified in sparse col '' (2397) of matrix 'A'.
Problem
  Name                   :                 
  Objective sense        : min             
  Type                   : CONIC (conic optimization problem)
  Constraints            : 631             
  Cones                  : 600             
  Scalar variables       : 2399            
  Matrix variables       : 0               
  Integer variables      : 0               

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries                  : 1                 time                   : 0.00            
Lin. dep.  - tries                  : 1                 time                   : 0.00            
Lin. dep.  - number                 : 0               
Presolve terminated. Time: 0.01    
Problem
  Name                   :                 
  Objective sense        : min             
  Type                   : CONIC (conic optimization problem)
  Constraints            : 631             
  Cones                  : 600             
  Scalar variables       : 2399            
  Matrix variables       : 0               
  Integer variables      : 0               

Optimizer  - threads                : 8               
Optimizer  - solved problem         : the primal      
Optimizer  - Constraints            : 31
Optimizer  - Cones                  : 600
Optimizer  - Scalar variables       : 1798              conic                  : 1798            
Optimizer  - Semi-definite variables: 0                 scalarized             : 0               
Factor     - setup time             : 0.00              dense det. time        : 0.00            
Factor     - ML order time          : 0.00              GP order time          : 0.00            
Factor     - nonzeros before factor : 496               after factor           : 496             
Factor     - dense dim.             : 0                 flops                  : 1.72e+06        
ITE PFEAS    DFEAS    GFEAS    PRSTATUS   POBJ              DOBJ              MU       TIME  
0   6.0e+02  1.0e+00  1.0e+00  0.00e+00   0.000000000e+00   0.000000000e+00   1.0e+00  0.01  
1   5.6e+01  9.3e-02  2.3e-02  -1.86e-02  -1.053247766e+00  -1.107657093e+00  9.3e-02  0.02  
2   1.4e+01  2.4e-02  5.1e-03  7.43e+00   -1.869314281e-01  -1.462303815e-01  2.4e-02  0.02  
3   3.9e+00  6.4e-03  5.2e-04  1.67e+00   -1.134293468e-01  -1.076707815e-01  6.4e-03  0.02  
4   1.0e+00  1.7e-03  4.7e-05  1.23e+00   -9.870405328e-02  -9.809674395e-02  1.7e-03  0.03  
5   2.8e-01  4.6e-04  5.2e-06  1.05e+00   -9.678705753e-02  -9.670866622e-02  4.6e-04  0.03  
6   8.2e-02  1.4e-04  6.3e-07  1.01e+00   -9.650438591e-02  -9.649676640e-02  1.4e-04  0.03  
7   2.1e-02  3.5e-05  6.3e-08  1.00e+00   -9.643505521e-02  -9.643532474e-02  3.5e-05  0.03  
8   5.4e-03  9.1e-06  6.0e-09  1.00e+00   -9.642852754e-02  -9.642898680e-02  9.1e-06  0.03  
9   8.2e-04  1.4e-06  3.3e-10  1.00e+00   -9.642658961e-02  -9.642666784e-02  1.4e-06  0.03  
10  8.8e-05  1.5e-07  1.1e-11  1.00e+00   -9.642630830e-02  -9.642631732e-02  1.5e-07  0.04  
11  1.2e-05  2.1e-08  5.5e-13  1.00e+00   -9.642628483e-02  -9.642628618e-02  2.1e-08  0.04  
12  1.9e-06  3.1e-09  2.9e-14  1.00e+00   -9.642628194e-02  -9.642628217e-02  3.1e-09  0.04  
13  2.1e-07  3.5e-10  8.6e-16  1.00e+00   -9.642628168e-02  -9.642628171e-02  3.5e-10  0.04  
Optimizer terminated. Time: 0.05    


Interior-point solution summary
  Problem status  : PRIMAL_AND_DUAL_FEASIBLE
  Solution status : OPTIMAL
  Primal.  obj: -9.6426281680e-02   nrm: 1e+00    Viol.  con: 2e-08    var: 0e+00    cones: 0e+00  
  Dual.    obj: -9.6426281708e-02   nrm: 8e-01    Viol.  con: 0e+00    var: 3e-11    cones: 0e+00  
Optimizer summary
  Optimizer                 -                        time: 0.05    
    Interior-point          - iterations : 13        time: 0.04    
      Basis identification  -                        time: 0.00    
        Primal              - iterations : 0         time: 0.00    
        Dual                - iterations : 0         time: 0.00    
        Clean primal        - iterations : 0         time: 0.00    
        Clean dual          - iterations : 0         time: 0.00    
    Simplex                 -                        time: 0.00    
      Primal simplex        - iterations : 0         time: 0.00    
      Dual simplex          - iterations : 0         time: 0.00    
    Mixed integer           - relaxations: 0         time: 0.00    

------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0.0964263
 
Frequency equalization problem is Solved
 
Calling Mosek 9.1.9: 115 variables, 69 equality constraints
   For improved efficiency, Mosek is solving the dual problem.
------------------------------------------------------------

MOSEK Version 9.1.9 (Build date: 2019-11-21 11:32:15)
Copyright (c) MOSEK ApS, Denmark. WWW: mosek.com
Platform: MACOSX/64-X86

Problem
  Name                   :                 
  Objective sense        : min             
  Type                   : CONIC (conic optimization problem)
  Constraints            : 69              
  Cones                  : 38              
  Scalar variables       : 115             
  Matrix variables       : 0               
  Integer variables      : 0               

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries                  : 1                 time                   : 0.00            
Lin. dep.  - tries                  : 1                 time                   : 0.00            
Lin. dep.  - number                 : 0               
Presolve terminated. Time: 0.00    
Problem
  Name                   :                 
  Objective sense        : min             
  Type                   : CONIC (conic optimization problem)
  Constraints            : 69              
  Cones                  : 38              
  Scalar variables       : 115             
  Matrix variables       : 0               
  Integer variables      : 0               

Optimizer  - threads                : 8               
Optimizer  - solved problem         : the primal      
Optimizer  - Constraints            : 31
Optimizer  - Cones                  : 39
Optimizer  - Scalar variables       : 78                conic                  : 78              
Optimizer  - Semi-definite variables: 0                 scalarized             : 0               
Factor     - setup time             : 0.00              dense det. time        : 0.00            
Factor     - ML order time          : 0.00              GP order time          : 0.00            
Factor     - nonzeros before factor : 286               after factor           : 316             
Factor     - dense dim.             : 0                 flops                  : 1.04e+04        
ITE PFEAS    DFEAS    GFEAS    PRSTATUS   POBJ              DOBJ              MU       TIME  
0   3.7e+01  1.0e+00  1.0e+00  0.00e+00   0.000000000e+00   0.000000000e+00   1.0e+00  0.00  
1   1.8e+01  4.8e-01  6.8e-02  2.88e+00   -2.068370829e-03  -1.751009111e-01  4.8e-01  0.01  
2   1.4e+01  3.8e-01  6.3e-02  1.04e+01   -3.821493574e-03  -1.475861758e-02  3.8e-01  0.01  
3   9.9e+00  2.7e-01  3.8e-02  1.80e+00   -1.616184168e-02  -2.124433938e-02  2.7e-01  0.01  
4   2.7e+00  7.4e-02  5.7e-03  1.46e+00   -2.872004696e-02  -2.903709348e-02  7.4e-02  0.01  
5   6.5e-01  1.8e-02  6.5e-04  1.08e+00   -3.114938952e-02  -3.126758284e-02  1.8e-02  0.01  
6   1.2e-01  3.2e-03  4.7e-05  1.02e+00   -3.156009869e-02  -3.160204324e-02  3.2e-03  0.01  
7   1.9e-02  5.1e-04  2.6e-06  1.00e+00   -3.161464641e-02  -3.162942988e-02  5.1e-04  0.01  
8   3.4e-03  9.1e-05  1.9e-07  1.00e+00   -3.162308381e-02  -3.162635321e-02  9.1e-05  0.01  
9   4.1e-04  1.1e-05  7.4e-09  1.00e+00   -3.162468591e-02  -3.162515599e-02  1.1e-05  0.01  
10  7.5e-05  2.0e-06  5.6e-10  1.00e+00   -3.162497479e-02  -3.162506360e-02  2.0e-06  0.01  
11  2.2e-06  6.0e-08  2.4e-12  1.00e+00   -3.162504617e-02  -3.162504948e-02  6.0e-08  0.01  
12  4.3e-09  1.2e-10  2.1e-16  1.00e+00   -3.162504870e-02  -3.162504871e-02  1.2e-10  0.01  
Optimizer terminated. Time: 0.02    


Interior-point solution summary
  Problem status  : PRIMAL_AND_DUAL_FEASIBLE
  Solution status : OPTIMAL
  Primal.  obj: -3.1625048699e-02   nrm: 1e+00    Viol.  con: 4e-10    var: 0e+00    cones: 0e+00  
  Dual.    obj: -3.1625048706e-02   nrm: 8e-01    Viol.  con: 0e+00    var: 2e-13    cones: 0e+00  
Optimizer summary
  Optimizer                 -                        time: 0.02    
    Interior-point          - iterations : 12        time: 0.01    
      Basis identification  -                        time: 0.00    
        Primal              - iterations : 0         time: 0.00    
        Dual                - iterations : 0         time: 0.00    
        Clean primal        - iterations : 0         time: 0.00    
        Clean dual          - iterations : 0         time: 0.00    
    Simplex                 -                        time: 0.00    
      Primal simplex        - iterations : 0         time: 0.00    
      Dual simplex          - iterations : 0         time: 0.00    
    Mixed integer           - relaxations: 0         time: 0.00    

------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0.031625