n = 10;
wpass = 0.12*pi;
wstop = 0.24*pi;
atten_level = -30;
N = 30*n+1;
w = linspace(0,pi,N);
A = [ones(N,1) 2*cos(kron(w',[1:n]))];
ind = find((0 <= w) & (w <= wpass));
Ap = A(ind,:);
ind = find((wstop <= w) & (w <= pi));
Us = 10^(atten_level/20)*ones(length(ind),1);
As = A(ind,:);
cvx_begin
variable delta
variable h(n+1,1);
minimize( delta )
subject to
Ap*h <= delta;
inv_pos(Ap*h) <= delta;
abs( As*h ) <= Us;
cvx_end
disp(['Problem is ' cvx_status])
if ~strfind(cvx_status,'Solved')
return
else
h = [flipud(h(2:end)); h];
fprintf(1,'The optimal minimum passband ripple is %4.3f dB.\n\n',...
20*log10(delta));
end
figure(1)
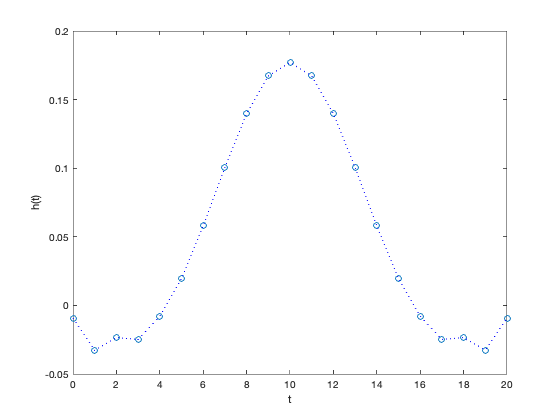
plot([0:2*n],h','o',[0:2*n],h','b:')
xlabel('t'), ylabel('h(t)')
figure(2)
H = exp(-j*kron(w',[0:2*n]))*h;
subplot(2,1,1)
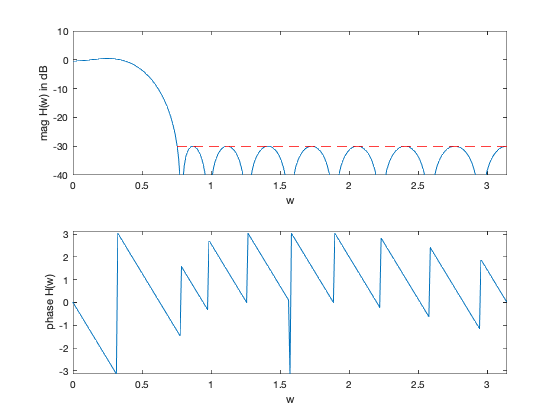
plot(w,20*log10(abs(H)),[wstop pi],[atten_level atten_level],'r--');
axis([0,pi,-40,10])
xlabel('w'), ylabel('mag H(w) in dB')
subplot(2,1,2)
plot(w,angle(H))
axis([0,pi,-pi,pi])
xlabel('w'), ylabel('phase H(w)')
Calling Mosek 9.1.9: 872 variables, 278 equality constraints
For improved efficiency, Mosek is solving the dual problem.
------------------------------------------------------------
MOSEK Version 9.1.9 (Build date: 2019-11-21 11:32:15)
Copyright (c) MOSEK ApS, Denmark. WWW: mosek.com
Platform: MACOSX/64-X86
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col '' (15) of matrix 'A'.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col '' (25) of matrix 'A'.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col '' (30) of matrix 'A'.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col '' (348) of matrix 'A'.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col '' (378) of matrix 'A'.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col '' (393) of matrix 'A'.
MOSEK warning 710: #3 (nearly) zero elements are specified in sparse col '' (420) of matrix 'A'.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col '' (450) of matrix 'A'.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col '' (480) of matrix 'A'.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col '' (520) of matrix 'A'.
Warning number 710 is disabled.
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 278
Cones : 266
Scalar variables : 872
Matrix variables : 0
Integer variables : 0
Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 1 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.00
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 278
Cones : 266
Scalar variables : 872
Matrix variables : 0
Integer variables : 0
Optimizer - threads : 8
Optimizer - solved problem : the primal
Optimizer - Constraints : 12
Optimizer - Cones : 266
Optimizer - Scalar variables : 606 conic : 569
Optimizer - Semi-definite variables: 0 scalarized : 0
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 78 after factor : 78
Factor - dense dim. : 0 flops : 8.21e+04
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 1.8e+01 2.0e+00 8.2e+00 0.00e+00 7.241615842e+00 0.000000000e+00 1.0e+00 0.00
1 2.8e+00 3.1e-01 2.3e+00 -8.75e-01 -1.998945020e+00 -3.617243608e+00 1.5e-01 0.01
2 1.9e+00 2.1e-01 2.0e-01 3.99e+00 -8.200931048e-01 -1.846272277e+00 1.0e-01 0.01
3 9.3e-01 1.0e-01 6.1e-02 4.53e+00 -1.058124331e+00 -1.195202409e+00 5.0e-02 0.01
4 3.1e-01 3.4e-02 1.0e-02 1.61e+00 -1.052999195e+00 -1.089169990e+00 1.7e-02 0.01
5 1.9e-01 2.0e-02 4.3e-03 1.25e+00 -1.051899834e+00 -1.072726061e+00 1.0e-02 0.01
6 5.8e-02 6.2e-03 7.1e-04 1.16e+00 -1.048919009e+00 -1.055053535e+00 3.1e-03 0.02
7 2.1e-02 2.3e-03 1.4e-04 1.04e+00 -1.050974672e+00 -1.053297408e+00 1.2e-03 0.02
8 6.3e-03 6.8e-04 2.0e-05 1.02e+00 -1.051455740e+00 -1.052152763e+00 3.4e-04 0.02
9 3.1e-03 3.4e-04 6.6e-06 1.00e+00 -1.051520602e+00 -1.051867788e+00 1.7e-04 0.02
10 9.5e-04 1.0e-04 1.1e-06 1.00e+00 -1.051547782e+00 -1.051653646e+00 5.1e-05 0.02
11 5.0e-04 5.4e-05 3.8e-07 1.00e+00 -1.051557544e+00 -1.051612973e+00 2.7e-05 0.02
12 1.4e-04 1.5e-05 5.4e-08 1.00e+00 -1.051566841e+00 -1.051582143e+00 7.4e-06 0.02
13 3.5e-05 3.8e-06 6.4e-09 1.00e+00 -1.051575400e+00 -1.051579376e+00 1.9e-06 0.02
14 6.5e-06 7.0e-07 5.0e-10 1.00e+00 -1.051577416e+00 -1.051578147e+00 3.5e-07 0.02
15 1.0e-06 1.1e-07 3.2e-11 1.00e+00 -1.051577905e+00 -1.051578023e+00 5.6e-08 0.02
16 2.4e-08 2.6e-09 1.1e-13 1.00e+00 -1.051578005e+00 -1.051578007e+00 1.3e-09 0.02
Optimizer terminated. Time: 0.03
Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: -1.0515780047e+00 nrm: 1e+00 Viol. con: 2e-08 var: 0e+00 cones: 0e+00
Dual. obj: -1.0515780074e+00 nrm: 2e+00 Viol. con: 0e+00 var: 7e-10 cones: 0e+00
Optimizer summary
Optimizer - time: 0.03
Interior-point - iterations : 16 time: 0.02
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +1.05158
Problem is Solved
The optimal minimum passband ripple is 0.437 dB.