% Boyd, Kim, Vandenberghe, and Hassibi, "A Tutorial on Geometric Programming"
% Written for CVX by Almir Mutapcic 02/08/06
% (a figure is generated)
%
% Solves the problem of choosing gate scale factors x_i to give
% minimum ckt delay, subject to limits on the total area and power.
%
%   minimize   D
%       s.t.   P <= Pmax, A <= Amax
%              x >= 1
%
% where variables are scale factors x.
%
% This code uses matrices in order to evaluate signal paths
% through the circuit (thus, it uses vectorize Matlab features).
% It is specific to the digital circuit shown in figure 4 (page 28)
% of GP tutorial paper.

% digital circuit shown in figure 4 (page 28) of GP tutorial paper
m = 7;  % number of cells
n = 8;  % number of edges
A = sparse(m,n);

% A is standard cell-edge incidence matrix of the circuit
% A_ij = 1 if edge j comes out of cell i, -1 if it comes in, 0 otherwise
  A(1,1) =     1;
  A(2,2) =     1;
  A(2,3) =     1;
  A(3,4) =     1;
  A(3,8) =     1;
  A(4,1) =    -1;
  A(4,2) =    -1;
  A(4,5) =     1;
  A(4,6) =     1;
  A(5,3) =    -1;
  A(5,4) =    -1;
  A(5,7) =     1;
  A(6,5) =    -1;
  A(7,6) =    -1;
  A(7,7) =    -1;
  A(7,8) =    -1;

% decompose A into edge outgoing and edge-incoming part
Aout = double(A > 0);
Ain = double(A < 0);

% problem constants
f = [1 0.8 1 0.7 0.7 0.5 0.5]';
e = [1 2 1 1.5 1.5 1 2]';
Cout6 = 10;
Cout7 = 10;

a     = ones(m,1);
alpha = ones(m,1);
beta  = ones(m,1);
gamma = ones(m,1);

% varying parameters for an optimal trade-off curve
N = 20;
Pmax = linspace(10,100,N);
Amax = [25 50 100];
min_delay = zeros(length(Amax),N);

disp('Generating the optimal tradeoff curve...')

for k = 1:length(Amax)
    fprintf( 'Amax = %d:\n', Amax(k) );
    for n = 1:N
        fprintf( '    Pmax = %6.2f: ', Pmax(n) );
        cvx_begin gp quiet
          % optimization variables
          variable x(m)                 % scale factors
          variable t(m)                 % arrival times

          % objective is the upper bound on the overall delay
          % and that is the max of arrival times for output gates 6 and 7
          minimize( max( t(6),t(7) ) )
          subject to
            % input capacitance is an affine function of sizes
            cin = alpha + beta.*x;

            % load capacitance is the input capacitance times the fan-out matrix
            % given by Fout = Aout*Ain'
            cload = (Aout*Ain')*cin;
            cload(6) = Cout6;          % load capacitance of the output gate 6
            cload(7) = Cout7;          % load capacitance of othe utput gate 7

            % delay is the product of its driving resistance R = gamma./x and cload
            d = cload.*gamma./x;

            % power and area definitions
            power = (f.*e)'*x;
            area = a'*x;

            % scale size, power, and area constraints
            x >= 1;
            power <= Pmax(n);
            area <= Amax(k);

            % create timing constraints
            % these constraints enforce t_j + d_j <= t_i over all gates j that drive gate i
            Aout'*t + Ain'*d <= Ain'*t;

            % for gates with inputs not connected to other gates we enforce d_i <= t_i
            d(1:3) <= t(1:3);
        cvx_end
        fprintf( 'delay = %3.2f\n', cvx_optval );
        min_delay(k,n) = cvx_optval;
    end
end

% plot the tradeoff curve
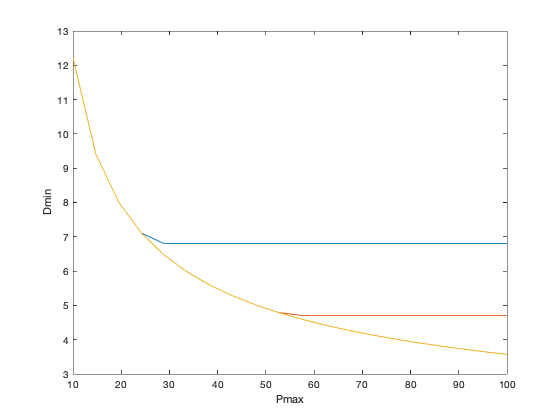
plot(Pmax,min_delay(1,:), Pmax,min_delay(2,:), Pmax,min_delay(3,:));
xlabel('Pmax'); ylabel('Dmin');
disp('Optimal tradeoff curve plotted.')

Generating the optimal tradeoff curve...
Amax = 25:
    Pmax =  10.00: delay = 12.21
    Pmax =  14.74: delay = 9.41
    Pmax =  19.47: delay = 8.01
    Pmax =  24.21: delay = 7.11
    Pmax =  28.95: delay = 6.80
    Pmax =  33.68: delay = 6.80
    Pmax =  38.42: delay = 6.80
    Pmax =  43.16: delay = 6.80
    Pmax =  47.89: delay = 6.80
    Pmax =  52.63: delay = 6.80
    Pmax =  57.37: delay = 6.80
    Pmax =  62.11: delay = 6.80
    Pmax =  66.84: delay = 6.80
    Pmax =  71.58: delay = 6.80
    Pmax =  76.32: delay = 6.80
    Pmax =  81.05: delay = 6.80
    Pmax =  85.79: delay = 6.80
    Pmax =  90.53: delay = 6.80
    Pmax =  95.26: delay = 6.80
    Pmax = 100.00: delay = 6.80
Amax = 50:
    Pmax =  10.00: delay = 12.21
    Pmax =  14.74: delay = 9.41
    Pmax =  19.47: delay = 8.01
    Pmax =  24.21: delay = 7.11
    Pmax =  28.95: delay = 6.46
    Pmax =  33.68: delay = 5.97
    Pmax =  38.42: delay = 5.59
    Pmax =  43.16: delay = 5.27
    Pmax =  47.89: delay = 5.01
    Pmax =  52.63: delay = 4.79
    Pmax =  57.37: delay = 4.71
    Pmax =  62.11: delay = 4.71
    Pmax =  66.84: delay = 4.71
    Pmax =  71.58: delay = 4.71
    Pmax =  76.32: delay = 4.71
    Pmax =  81.05: delay = 4.71
    Pmax =  85.79: delay = 4.71
    Pmax =  90.53: delay = 4.71
    Pmax =  95.26: delay = 4.71
    Pmax = 100.00: delay = 4.71
Amax = 100:
    Pmax =  10.00: delay = 12.21
    Pmax =  14.74: delay = 9.41
    Pmax =  19.47: delay = 8.01
    Pmax =  24.21: delay = 7.11
    Pmax =  28.95: delay = 6.46
    Pmax =  33.68: delay = 5.97
    Pmax =  38.42: delay = 5.59
    Pmax =  43.16: delay = 5.27
    Pmax =  47.89: delay = 5.01
    Pmax =  52.63: delay = 4.79
    Pmax =  57.37: delay = 4.60
    Pmax =  62.11: delay = 4.43
    Pmax =  66.84: delay = 4.28
    Pmax =  71.58: delay = 4.15
    Pmax =  76.32: delay = 4.03
    Pmax =  81.05: delay = 3.92
    Pmax =  85.79: delay = 3.82
    Pmax =  90.53: delay = 3.73
    Pmax =  95.26: delay = 3.65
    Pmax = 100.00: delay = 3.57
Optimal tradeoff curve plotted.