% Joëlle Skaf - 04/24/08
% (a figure is generated)
%
% Suppose y \in\reals^n is a Gaussian random variable with zero mean and
% covariance matrix R = \Expect(yy^T), with sparse inverse S = R^{-1}
% (S_ij = 0 means that y_i and y_j are conditionally independent).
% We want to estimate the covariance matrix R based on N independent
% samples y1,...,yN drawn from the distribution, and using prior knowledge
% that S is sparse
% A good heuristic for estimating R is to solve the problem
%           maximize    logdet(S) - tr(SY) - lambda*sum(sum(abs(S)))
%           subject to  S >= 0
% where Y is the sample covariance of y1,...,yN, and lambda is a sparsity
% parameter to be chosen or tuned.
% A figure showing the sparsity (number of nonzeros) of S versus lambda
% is generated.

% Input data
randn('state',0);
n = 10;
N = 100;
Strue = sprandsym(n,0.5,0.01,1);
nnz_true = sum(Strue(:)>1e-4);
R = inv(full(Strue));
y_sample = sqrtm(R)*randn(n,N);
Y = cov(y_sample');
Nlambda = 20;
lambda = logspace(-2, 3, Nlambda);
nnz = zeros(1,Nlambda);

for i=1:Nlambda
    disp(['i = ' num2str(i) ', lambda(i) = ' num2str(lambda(i))]);
    % Maximum likelihood estimate of R^{-1}
    cvx_begin sdp quiet
        variable S(n,n) symmetric
        maximize log_det(S) - trace(S*Y) - lambda(i)*sum(sum(abs(S)))
        S >= 0
    cvx_end
    nnz(i) = sum(S(:)>1e-4);
end

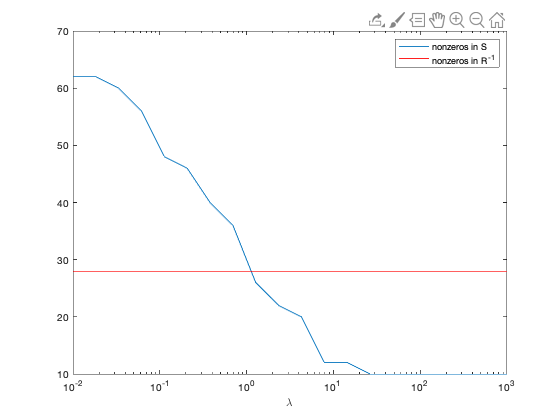
figure;
semilogx(lambda, nnz);
hold on;
semilogx(lambda, nnz_true*ones(1,Nlambda),'r');
xlabel('\lambda');
legend('nonzeros in S', 'nonzeros in R^{-1}');

i = 1, lambda(i) = 0.01
i = 2, lambda(i) = 0.01833
i = 3, lambda(i) = 0.033598
i = 4, lambda(i) = 0.061585
i = 5, lambda(i) = 0.11288
i = 6, lambda(i) = 0.20691
i = 7, lambda(i) = 0.37927
i = 8, lambda(i) = 0.69519
i = 9, lambda(i) = 1.2743
i = 10, lambda(i) = 2.3357
i = 11, lambda(i) = 4.2813
i = 12, lambda(i) = 7.8476
i = 13, lambda(i) = 14.3845
i = 14, lambda(i) = 26.3665
i = 15, lambda(i) = 48.3293
i = 16, lambda(i) = 88.5867
i = 17, lambda(i) = 162.3777
i = 18, lambda(i) = 297.6351
i = 19, lambda(i) = 545.5595
i = 20, lambda(i) = 1000