Demo: Sparse SVM

Contents

Support Vector Machine (SVM) example

We have binary data, and the two classes are labeled +1 and -1. The data is d-dimensional, and we have n samples. This example show show to solve the standard SVM using the hinge-loss and (\ell_2) penalty. Then it shows how it is easy with TFOCS to generalize the SVM problem and use the (\ell_1) penalty instead of the (\ell_2) penalty, which has the effect of encouraging sparsity. For a more detailed example, see the /examples/largescale/demo_SVM.m code in the TFOCS release. You can also download the source for this demo and try it yourself. 
% Before running this, please add the TFOCS base directory to your path
addpath ~/Dropbox/TFOCS/

Generate a new problem

randn('state',23432);
rand('state',3454);

n = 30;
d = 2; % 2D data is nice because it's easy to visualize

n1 = round(.5*n);   % number of -1 (this is data from one "class")
n2 = n - n1;        % number of +1 (this is data from the other "class")

% Generate data
mean1   = [-.5,1];
% mean2 = [.6,.2]; % can be separated
mean2   = [.1,.5]; % cannot be separated, so a bit more interesting
s       = .25;  % standard deviation
x1  = repmat(mean1,n1,1) + s*randn(n1,2);
x2  = repmat(mean2,n2,1) + s*randn(n2,2);

X = [x1; x2];
labels = [ ones(n1,1); -ones(n2,1) ];

% Plot the data:
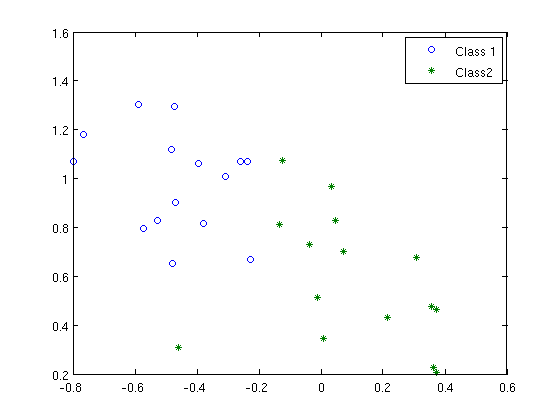
figure(1); clf;
hh = {};
hh{1}=plot(x1(:,1), x1(:,2), 'o' );
hold all
hh{2}=plot(x2(:,1), x2(:,2), '*' );
legend('Class 1','Class 2');
xl = get(gca,'xlim');
yl = get(gca,'ylim');
legend([hh{1:2}],'Class 1','Class2');

Introduce the SVM problem formulations

The hinge-loss can be defined in Matlab as: 
hinge = @(x) sum(max(0,1-x));
To see what it looks like: 
grid = linspace(-2,2,30);
figure(2);
plot( grid, max(0,1-grid) )
ylim( [-.5,3] ); set(gcf,'Position',[100,100,350,250] );
Then the standard SVM in primal form is the following: minimize_{m,b} hinge( labels.( Xm – b ) ) + lambda_A*norm(m,2) or in mathematical notation, (\min_{m,b} \sum_{i=1}^n\text{hinge}(\text{label}_i \cdot ( x_i^T m – b ) ) + \lambda_A |m|_2 ) where X is the data matrix (dimensions n x d ), m is the slope (dimension d x 1 ), and b is an offset (dimension 1 for our example). To put this in a more amenable format, introduce the variable “a” and let a = [m;b], so “a” has dimensions (d+1) x 1. Then we can express “Xm-b” as “[X,-ones(n,1)]a”. For this reason, we introduce the following linear operator: 
linearF     = diag(labels)*[ X, -ones(n,1) ];
So now, the problem is: minimize_{a} hinge( linearFa ) + lambda_Anorm( [ones(d,1); 0] * a ) or in semi-mathematical notation, (\min_{a} \text{hinge}( \text{linearF}\cdot a ) + \lambda_A |a(1:d)|_2 ) (in the “norm” term, we want a 0 term in front of a(d+1) since we do not wish to penalize the norm of the constant offset). A reasonable value of lambda_A is: 
lambda_A    = 10;

Introduce the sparse SVM formulation

The sparse SVM is designed to induce sparsity in the slope variable m by replacing the lambda_Anorm(m,2) term with a lambda_Bnorm(m,1) term, since the l1 term drives small coefficients to zero. The optimization problem is (\min_{m,b} \sum_{i=1}^n\text{hinge}(\text{label}_i \cdot ( x_i^T m – b ) ) + \lambda_B |m|_1 ) Here’s a reasomable value for lambda_B: 
lambda_B    = 4;

Solve SVM

mu          = 1e-2;     % smoothing parameter
Dualize the hinge loss and the l2 terms: 
prox        = { prox_hingeDual(1,1,-1), proj_l2(lambda_A) };
Make the affine operator: 
offset1     = [];
linearF2    = diag( [ones(d,1);0] );
offset2     = [];
affineF     = { linearF, offset1; linearF2, offset2 };
ak          = tfocs_SCD([],affineF, prox, mu);
Auslender & Teboulle's single-projection method
Iter    Objective   |dx|/|x|    step
----+----------------------------------
100 | +6.32155e+00  2.55e-02  6.73e-04
200 | +1.83227e+01  1.21e-02  1.64e-03
300 | +2.69868e+01  1.74e-03  3.05e-03
322 | +2.73483e+01  2.74e-08  1.26e-12*
Finished: Unexpectedly small stepsize
Plot 
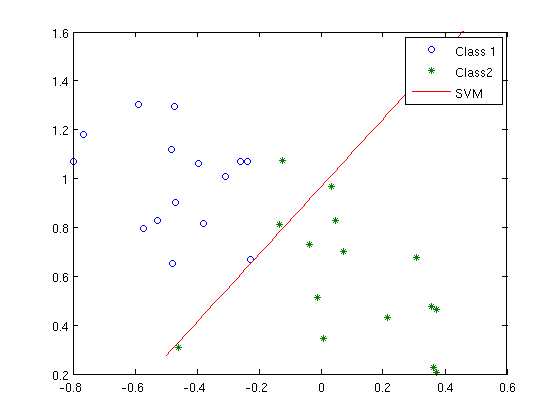
m       = ak(1:2); % slope
b       = ak(3);   % intercept
grid    = linspace(-.5,1,100);
figure(1);
hh{3}   = plot( grid, (b-m(1)*grid)/m(2) );
xlim(xl); ylim(yl);
legend([hh{1:3}],'Class 1','Class2','SVM');

Solve Sparse SVM

PROBLEM     = 2;
mu          = 1e-2;     % smoothing parameter
opts        = [];
opts.tol    = 1e-3;
Dualize the hinge loss to get ‘prox_hingeDual’ For the hingeDual, scale by -1 since we want polar cone, not dual cone Dualize the l1 term to get the linf term 
prox        = { prox_hingeDual(1,1,-1), proj_linf(lambda_B) };
linearF2    = diag( [ones(d,1);0] );
ak          = tfocs_SCD([],{linearF,[];linearF2,[]}, prox, mu,[],[],opts);
Auslender & Teboulle's single-projection method
Iter    Objective   |dx|/|x|    step
----+----------------------------------
100 | +6.32155e+00  2.55e-02  6.73e-04
200 | +1.72515e+01  5.76e-03  1.64e-03
300 | +2.05441e+01  1.57e-03  4.85e-03
304 | +2.06012e+01  8.85e-04  1.85e-03
Finished: Step size tolerance reached
Plot 
m       = ak(1:2); % slope
b       = ak(3);   % intercept
grid    = linspace(-.5,1,100);
hh{4}   = plot( grid, (b-m(1)*grid)/m(2) );
xlim(xl); ylim(yl);
legend([hh{:}],'Class 1','Class2','SVM','sparse SVM');
You can see that the sparse SVM hyperplane is vertical! This is because the x-component is zero, and only the y-component is non-zero. So it is “sparse” (though in this 2D example, “sparsity” doesn’t mean much). For larger dimensional data, the idea is that identifying a hyperplane that only has a few non-zeros will allow you to identify which dimensions are actually important. TFOCS v1.1 by Stephen Becker, Emmanuel Candes, and Michael Grant. Copyright 2012 California Institute of Technology and CVX Research. See the file TFOCS/license.{txt,pdf} for full license information. Published with MATLAB® 7.12