% Section 5.4,  L. Vandenberghe, S. Boyd, and A. El Gamal
% "Optimizing dominant time constant in RC circuits"
% Original by Lieven Vandenberghe
% Adapted for CVX by Joelle Skaf - 11/27/05
% Modified by Michael Grant - 3/8/06
%
% We optimize a tri-state bus connecting six nodes ( The model for the bus
% is shown in the paper, fig.16). The total wire area is sum_{i>j} lij*xij
% The bus can be driven from any node. When node i drives the bus, the ith
% switch is closed and the others are all open. Thus we really have six
% different circuits, each corresponding to a given node driving the bus.
% we require that the dominant time constant of each of the six drive
% configuration circuits has dominant time constant less than Tmax.
% The problem can be formulated with the following SDP:
%               minimize        sum_{i>j}(x_ij*l_ij)
%                   s.t.        0 <= xij <= wmax
%                               Tmax*(G(x) + GE_kk) - C(x) >= 0 , 1 <=k<= 6
% The matrix E_kk is zero except for the kth diagonal element, which is 1.

%
% Circuit parameters
%

n=6;         % number of nodes
m=15;        % number of wires
beta = 0.5;  % capacitance per segment is twice beta times xi*li
alpha = 1;   % conductance per segment is alpha times xi/li
G0 = 1;      % source conductance
C0 = 10;     % load capacitor
wmax = 1;    % upper bound on x

%
% Node positions
%

xpos = [ 0   1   6   8  -4  -1 ;
         0  -1   4  -2   1   4 ] ;
X11 = repmat(xpos(1,:),n,1);
X12 = repmat(xpos(1,:)',1,n);
X21 = repmat(xpos(2,:),n,1);
X22 = repmat(xpos(2,:)',1,n);
LL  = abs(X11-X12) + abs(X21-X22);
L   = tril(LL);
L   = L(L>0);

%
% Construct the capacitance and conductance matrices
%   C(x) = C0 + w11 * C1 + w21 * C2 + ...
%   G(x) = G0 + w11 * G1 + w21 * G2 + ...
% and we assemble the coefficient matrices together as follows:
%   CC = [ C0(:) C1(:) C2(:) ... ]
%   GG = [ G0(:) G1(:) G2(:) ... ]
%

CC = zeros(n,n,m+1);
GG = zeros(n,n,m+1);
CC(:,:,1) = C0 * eye(n);
% segment capacitances and conductances
k3 = 1;
for k1 = 1 : 5,
    for k2 = k1 + 1 : 6,
        CC([k1,k2],[k1,k2],k3) = beta *[1, 0; 0,1]*L(k3);
        GG([k1,k2],[k1,k2],k3) = alpha*[1,-1;-1,1]/L(k3);
        k3 = k3 + 1;
    end
end
GG = reshape( GG, n*n, m+1 );
CC = reshape( CC, n*n, m+1 );

%
% Compute points the tradeoff curve and the two desired points
%

% points on the tradeoff curve
npts    = 50;
delays  = linspace( 410, 2000, npts );
xdelays = [ 410, 2000 ];
xnpts   = length(xdelays);
areas   = zeros(1,npts);
xareas  = zeros(1,xnpts);
sizes   = zeros(m,xnpts);
for i = 1 : npts  + xnpts,

    if i > npts,
        xi = i - npts;
        delay = xdelays(xi);
        disp( sprintf( 'Particular solution %d of %d (Tmax = %g)', xi, xnpts, delay ) );
    else
        delay = delays(i);
        disp( sprintf( 'Point %d of %d on the tradeoff curve (Tmax = %g)', i, npts, delay ) );
    end

    %
    % Construct and solve the convex model
    %

    cvx_begin sdp quiet
        variable x(m)
        variable G(n,n) symmetric
        variable C(n,n) symmetric
        minimize( L'*x )
        G == reshape( GG * [ 1 ; x ], n, n );
        C == reshape( CC * [ 1 ; x ], n, n );
        for k = 1 : n,
            delay * G - C + sparse(k,k,delay,n,n) >= 0;
        end
        0 <= x <= wmax;
    cvx_end

    if i <= npts,
        areas(i) = cvx_optval;
    else
        xareas(xi) = cvx_optval;
        sizes(:,xi) = x;

        %
        % Plot the step response
        %

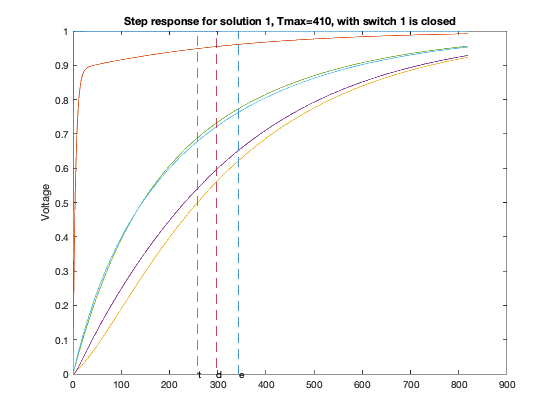
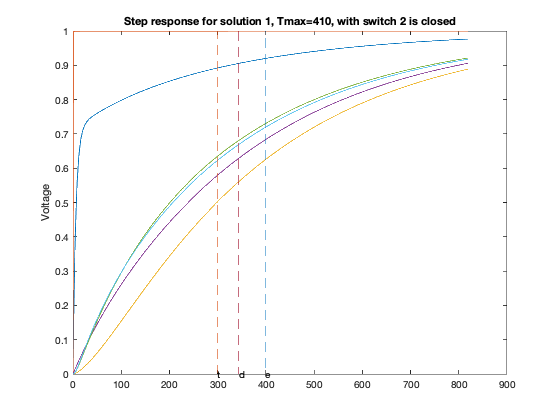
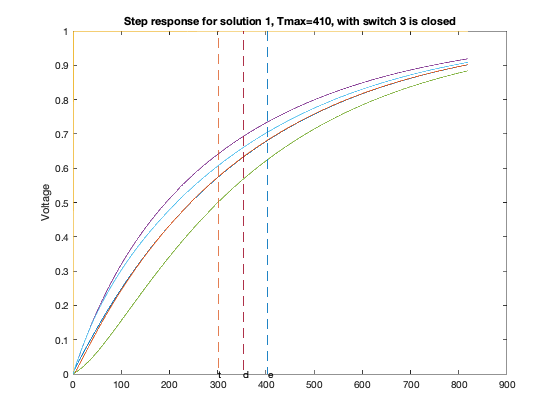
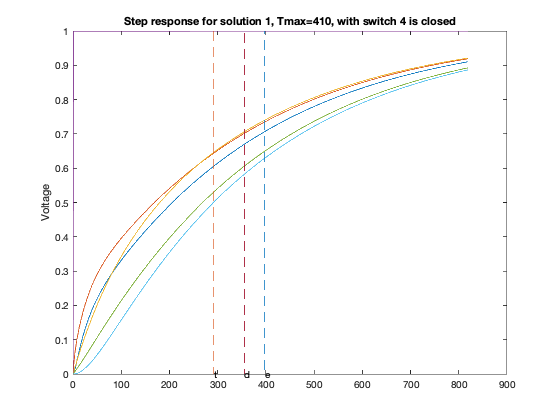
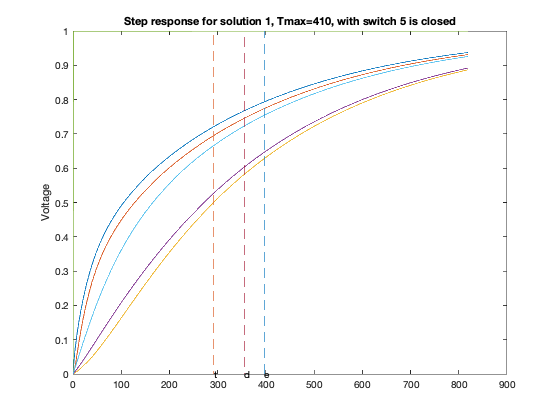
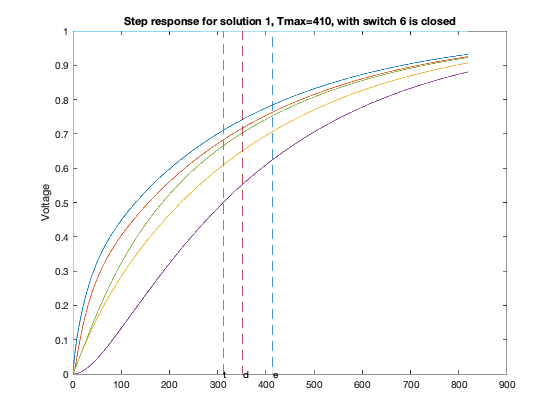
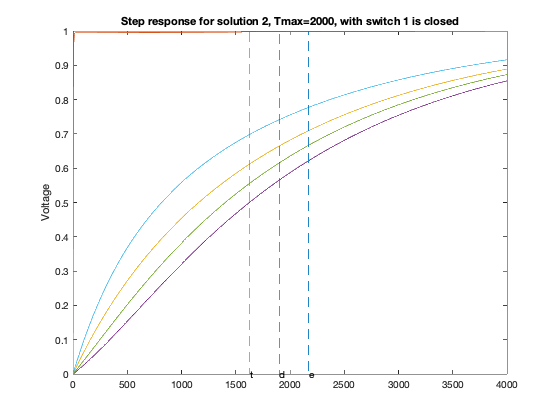
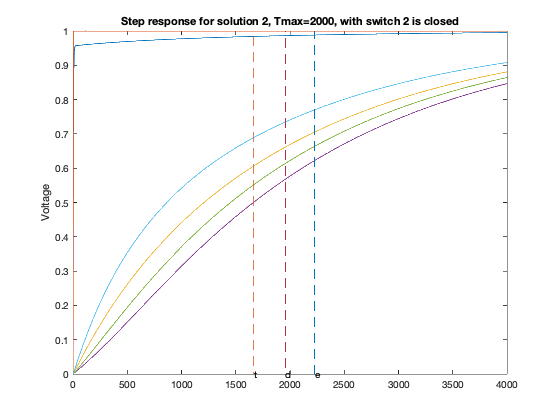
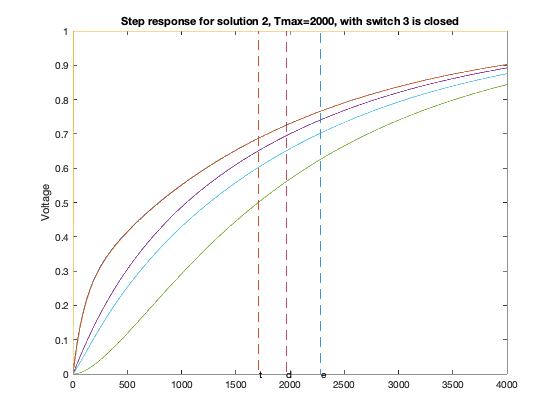
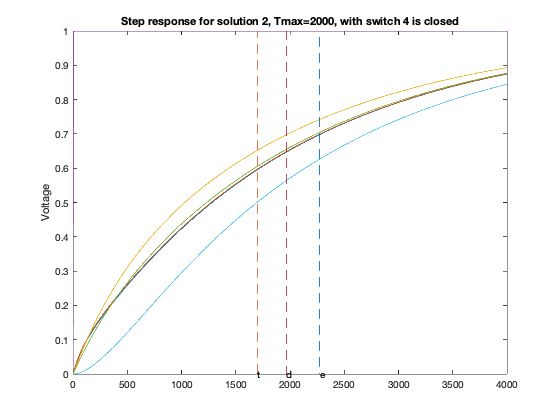
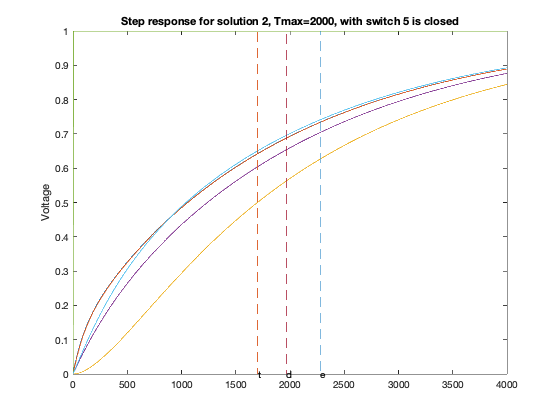
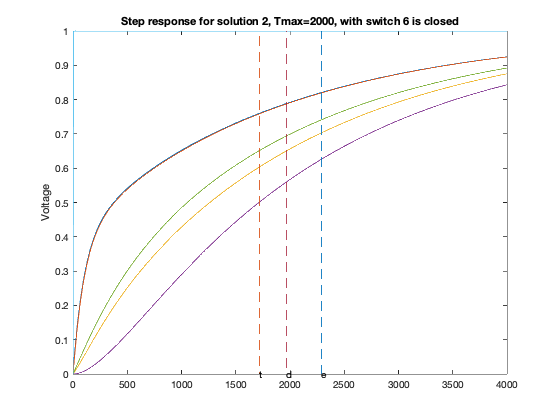
        T = linspace(0,2*delay,1000);
        for inp = 1 : 6,
            figure(6*xi-5+inp);
            GQ = G + sparse(inp,inp,delay,n,n);
            A = -inv(C)*GQ;
            B = -A*ones(n,1);
            Y = simple_step(A,B,T(2),length(T));
            hold off; plot(T,Y,'-');  hold on;
            ind=0;
            for j=1:size(Y,1),
                ind = max(min(find(Y(j,:)>=0.5)),ind);
            end
            tdom   = max(eig(inv(GQ)*C));
            elmore = max(sum((inv(GQ)*C)'));
            tthres = T(ind);
            plot( tdom   * [1;1], [0;1], '--', ...
                  elmore * [1;1], [0;1], '--', ...
                  tthres * [1;1], [0;1], '--');
            text(tdom,  0,'d');
            text(elmore,0,'e');
            text(tthres,0,'t');
            ylabel('Voltage');
            title(sprintf('Step response for solution %d, Tmax=%d, with switch %d is closed',xi,delay,inp));
       end

    end

end;

%
% Plot the tradeoff curve
%

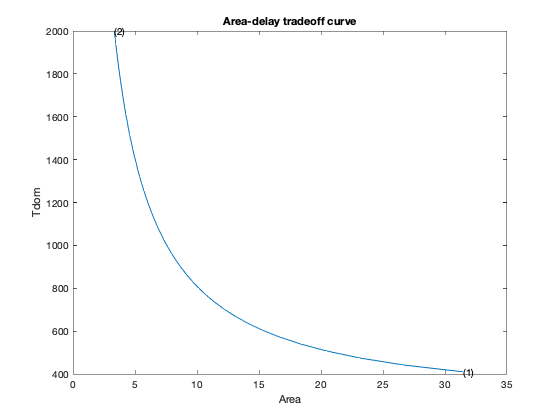
figure(1)
ind = isfinite(areas);
plot(areas(ind), delays(ind));
xlabel('Area');
ylabel('Tdom');
title('Area-delay tradeoff curve');
hold on
for k = 1 : xnpts,
    text( xareas(k), xdelays(k), sprintf( '(%d)', k ) );
end

Point 1 of 50 on the tradeoff curve (Tmax = 410)
Point 2 of 50 on the tradeoff curve (Tmax = 442.449)
Point 3 of 50 on the tradeoff curve (Tmax = 474.898)
Point 4 of 50 on the tradeoff curve (Tmax = 507.347)
Point 5 of 50 on the tradeoff curve (Tmax = 539.796)
Point 6 of 50 on the tradeoff curve (Tmax = 572.245)
Point 7 of 50 on the tradeoff curve (Tmax = 604.694)
Point 8 of 50 on the tradeoff curve (Tmax = 637.143)
Point 9 of 50 on the tradeoff curve (Tmax = 669.592)
Point 10 of 50 on the tradeoff curve (Tmax = 702.041)
Point 11 of 50 on the tradeoff curve (Tmax = 734.49)
Point 12 of 50 on the tradeoff curve (Tmax = 766.939)
Point 13 of 50 on the tradeoff curve (Tmax = 799.388)
Point 14 of 50 on the tradeoff curve (Tmax = 831.837)
Point 15 of 50 on the tradeoff curve (Tmax = 864.286)
Point 16 of 50 on the tradeoff curve (Tmax = 896.735)
Point 17 of 50 on the tradeoff curve (Tmax = 929.184)
Point 18 of 50 on the tradeoff curve (Tmax = 961.633)
Point 19 of 50 on the tradeoff curve (Tmax = 994.082)
Point 20 of 50 on the tradeoff curve (Tmax = 1026.53)
Point 21 of 50 on the tradeoff curve (Tmax = 1058.98)
Point 22 of 50 on the tradeoff curve (Tmax = 1091.43)
Point 23 of 50 on the tradeoff curve (Tmax = 1123.88)
Point 24 of 50 on the tradeoff curve (Tmax = 1156.33)
Point 25 of 50 on the tradeoff curve (Tmax = 1188.78)
Point 26 of 50 on the tradeoff curve (Tmax = 1221.22)
Point 27 of 50 on the tradeoff curve (Tmax = 1253.67)
Point 28 of 50 on the tradeoff curve (Tmax = 1286.12)
Point 29 of 50 on the tradeoff curve (Tmax = 1318.57)
Point 30 of 50 on the tradeoff curve (Tmax = 1351.02)
Point 31 of 50 on the tradeoff curve (Tmax = 1383.47)
Point 32 of 50 on the tradeoff curve (Tmax = 1415.92)
Point 33 of 50 on the tradeoff curve (Tmax = 1448.37)
Point 34 of 50 on the tradeoff curve (Tmax = 1480.82)
Point 35 of 50 on the tradeoff curve (Tmax = 1513.27)
Point 36 of 50 on the tradeoff curve (Tmax = 1545.71)
Point 37 of 50 on the tradeoff curve (Tmax = 1578.16)
Point 38 of 50 on the tradeoff curve (Tmax = 1610.61)
Point 39 of 50 on the tradeoff curve (Tmax = 1643.06)
Point 40 of 50 on the tradeoff curve (Tmax = 1675.51)
Point 41 of 50 on the tradeoff curve (Tmax = 1707.96)
Point 42 of 50 on the tradeoff curve (Tmax = 1740.41)
Point 43 of 50 on the tradeoff curve (Tmax = 1772.86)
Point 44 of 50 on the tradeoff curve (Tmax = 1805.31)
Point 45 of 50 on the tradeoff curve (Tmax = 1837.76)
Point 46 of 50 on the tradeoff curve (Tmax = 1870.2)
Point 47 of 50 on the tradeoff curve (Tmax = 1902.65)
Point 48 of 50 on the tradeoff curve (Tmax = 1935.1)
Point 49 of 50 on the tradeoff curve (Tmax = 1967.55)
Point 50 of 50 on the tradeoff curve (Tmax = 2000)
Particular solution 1 of 2 (Tmax = 410)
Particular solution 2 of 2 (Tmax = 2000)