randn('state',0);
m=100; n=30;
A = randn(m,n);
b = randn(m,1);
disp('ell-one approximation');
cvx_begin
variable x1(n)
minimize(norm(A*x1+b,1))
cvx_end
disp('ell-2');
x2=-A\b;
dz = 0.5;
disp('deadzone penalty');
cvx_begin
variable xdz(n)
minimize(sum(max(abs(A*xdz+b)-dz,0)))
cvx_end
disp('log-barrier')
alpha=.01; beta=.5;
cvx_begin
variable xlb(n)
minimize norm(A*xlb+b,Inf)
cvx_end
linf = cvx_optval;
A = A/(1.1*linf);
b = b/(1.1*linf);
for iters = 1:50
yp = 1 - (A*xlb+b); ym = (A*xlb+b) + 1;
f = -sum(log(yp)) - sum(log(ym));
g = A'*(1./yp) - A'*(1./ym);
H = A'*diag(1./(yp.^2) + 1./(ym.^2))*A;
v = -H\g;
fprime = g'*v;
ntdecr = sqrt(-fprime);
if (ntdecr < 1e-5), break; end;
t = 1;
newx = xlb + t*v;
while ((min(1-(A*newx +b)) < 0) | (min((A*newx +b)+1) < 0))
t = beta*t;
newx = xlb + t*v;
end;
newf = -sum(log(1 - (A*newx+b))) - sum(log(1+(A*newx+b)));
while (newf > f + alpha*t*fprime)
t = beta*t;
newx = xlb + t*v;
newf = -sum(log(1-(A*newx+b))) - sum(log(1+(A*newx+b)));
end;
xlb = xlb+t*v;
end
ss = max(abs([A*x1+b; A*x2+b; A*xdz+b; A*xlb+b]));
tt = -ceil(ss):0.05:ceil(ss);
[N1,hist1] = hist(A*x1+b,tt);
[N2,hist2] = hist(A*x2+b,tt);
[N3,hist3] = hist(A*xdz+b,tt);
[N4,hist4] = hist(A*xlb+b,tt);
range_max=2.0; rr=-range_max:1e-2:range_max;
figure(1), clf, hold off
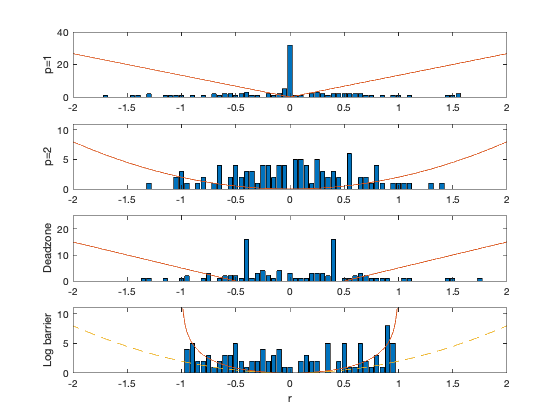
subplot(4,1,1),
bar(hist1,N1);
hold on
plot(rr, abs(rr)*40/3, '-');
ylabel('p=1')
axis([-range_max range_max 0 40]);
hold off
subplot(4,1,2),
bar(hist2,N2);
hold on;
plot(rr,2*rr.^2),
ylabel('p=2')
axis([-range_max range_max 0 11]);
hold off
subplot(4,1,3),
bar(hist3,N3);
hold on
plot(rr,30/3*max(0,abs(rr)-dz))
ylabel('Deadzone')
axis([-range_max range_max 0 25]);
hold off
subplot(4,1,4),
bar(hist4,N4);
rr_lb=linspace(-1+(1e-6),1-(1e-6),600);
hold on
plot(rr_lb, -3*log(1-rr_lb.^2),rr,2*rr.^2,'--')
axis([-range_max range_max 0 11]);
ylabel('Log barrier'),
xlabel('r')
hold off
ell-one approximation
Calling Mosek 9.1.9: 230 variables, 100 equality constraints
------------------------------------------------------------
MOSEK Version 9.1.9 (Build date: 2019-11-21 11:32:15)
Copyright (c) MOSEK ApS, Denmark. WWW: mosek.com
Platform: MACOSX/64-X86
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 100
Cones : 100
Scalar variables : 230
Matrix variables : 0
Integer variables : 0
Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 2 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.00
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 100
Cones : 100
Scalar variables : 230
Matrix variables : 0
Integer variables : 0
Optimizer - threads : 8
Optimizer - solved problem : the primal
Optimizer - Constraints : 100
Optimizer - Cones : 101
Optimizer - Scalar variables : 231 conic : 231
Optimizer - Semi-definite variables: 0 scalarized : 0
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 5050 after factor : 5050
Factor - dense dim. : 0 flops : 6.52e+05
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 9.1e-01 1.0e+00 1.0e+02 0.00e+00 1.000000000e+02 0.000000000e+00 1.0e+00 0.00
1 2.2e-01 2.4e-01 1.4e+01 2.80e-01 7.060624522e+01 3.784862497e+01 2.4e-01 0.01
2 3.4e-02 3.8e-02 9.5e-01 7.78e-01 5.768394141e+01 5.199419342e+01 3.8e-02 0.01
3 5.1e-03 5.6e-03 5.6e-02 9.60e-01 5.545706313e+01 5.459471232e+01 5.6e-03 0.01
4 7.9e-04 8.7e-04 3.4e-03 9.93e-01 5.518402336e+01 5.504930216e+01 8.7e-04 0.01
5 8.8e-05 9.7e-05 1.4e-04 9.99e-01 5.513415482e+01 5.511920868e+01 9.7e-05 0.01
6 5.2e-07 5.7e-07 6.5e-08 1.00e+00 5.512896399e+01 5.512887611e+01 5.7e-07 0.01
7 1.0e-09 1.1e-09 5.6e-12 1.00e+00 5.512892168e+01 5.512892151e+01 1.1e-09 0.01
Optimizer terminated. Time: 0.02
Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: 5.5128921677e+01 nrm: 2e+00 Viol. con: 3e-09 var: 0e+00 cones: 0e+00
Dual. obj: 5.5128921505e+01 nrm: 1e+00 Viol. con: 0e+00 var: 3e-10 cones: 0e+00
Optimizer summary
Optimizer - time: 0.02
Interior-point - iterations : 7 time: 0.01
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +55.1289
ell-2
deadzone penalty
Calling Mosek 9.1.9: 430 variables, 200 equality constraints
------------------------------------------------------------
MOSEK Version 9.1.9 (Build date: 2019-11-21 11:32:15)
Copyright (c) MOSEK ApS, Denmark. WWW: mosek.com
Platform: MACOSX/64-X86
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 200
Cones : 100
Scalar variables : 430
Matrix variables : 0
Integer variables : 0
Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 1 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.00
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 200
Cones : 100
Scalar variables : 430
Matrix variables : 0
Integer variables : 0
Optimizer - threads : 8
Optimizer - solved problem : the primal
Optimizer - Constraints : 200
Optimizer - Cones : 101
Optimizer - Scalar variables : 431 conic : 231
Optimizer - Semi-definite variables: 0 scalarized : 0
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 5250 after factor : 5250
Factor - dense dim. : 0 flops : 6.53e+05
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 1.0e+00 1.0e+00 1.0e+00 0.00e+00 0.000000000e+00 0.000000000e+00 1.0e+00 0.00
1 2.8e-01 2.8e-01 1.4e-01 1.27e+00 1.708375563e+01 1.706224635e+01 2.8e-01 0.01
2 4.4e-02 4.4e-02 7.6e-03 1.20e+00 2.038293662e+01 2.037532416e+01 4.4e-02 0.01
3 8.4e-03 8.4e-03 6.0e-04 1.02e+00 2.122013384e+01 2.121827348e+01 8.4e-03 0.01
4 1.5e-03 1.5e-03 4.3e-05 1.01e+00 2.141695065e+01 2.141659319e+01 1.5e-03 0.01
5 5.5e-05 5.5e-05 2.9e-07 1.00e+00 2.146633071e+01 2.146631299e+01 5.5e-05 0.01
6 5.2e-07 5.2e-07 2.6e-10 1.00e+00 2.146820113e+01 2.146820097e+01 5.2e-07 0.01
7 8.4e-11 5.1e-11 2.9e-17 1.00e+00 2.146821179e+01 2.146821179e+01 1.1e-11 0.01
Optimizer terminated. Time: 0.02
Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: 2.1468211791e+01 nrm: 2e+00 Viol. con: 2e-10 var: 7e-12 cones: 0e+00
Dual. obj: 2.1468211791e+01 nrm: 1e+00 Viol. con: 0e+00 var: 4e-11 cones: 0e+00
Optimizer summary
Optimizer - time: 0.02
Interior-point - iterations : 7 time: 0.01
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +21.4682
log-barrier
Calling Mosek 9.1.9: 300 variables, 131 equality constraints
For improved efficiency, Mosek is solving the dual problem.
------------------------------------------------------------
MOSEK Version 9.1.9 (Build date: 2019-11-21 11:32:15)
Copyright (c) MOSEK ApS, Denmark. WWW: mosek.com
Platform: MACOSX/64-X86
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 131
Cones : 100
Scalar variables : 300
Matrix variables : 0
Integer variables : 0
Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 1 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.00
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 131
Cones : 100
Scalar variables : 300
Matrix variables : 0
Integer variables : 0
Optimizer - threads : 8
Optimizer - solved problem : the primal
Optimizer - Constraints : 31
Optimizer - Cones : 100
Optimizer - Scalar variables : 200 conic : 200
Optimizer - Semi-definite variables: 0 scalarized : 0
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 496 after factor : 496
Factor - dense dim. : 0 flops : 2.03e+05
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 9.9e+01 2.0e+00 1.0e+00 0.00e+00 0.000000000e+00 0.000000000e+00 1.0e+00 0.00
1 9.6e+00 1.9e-01 2.1e-01 -9.30e-01 -8.854286451e+00 -4.886856194e+00 9.7e-02 0.01
2 2.4e+00 4.6e-02 8.3e-03 1.47e+00 -2.950577202e+00 -2.898027074e+00 2.4e-02 0.01
3 7.3e-01 1.4e-02 1.7e-03 3.00e+00 -1.463770043e+00 -1.421628806e+00 7.3e-03 0.01
4 2.0e-01 4.0e-03 2.3e-04 1.33e+00 -1.265556578e+00 -1.256021272e+00 2.0e-03 0.01
5 5.5e-02 1.1e-03 3.0e-05 1.09e+00 -1.217539111e+00 -1.215355835e+00 5.6e-04 0.01
6 1.2e-02 2.4e-04 2.5e-06 1.03e+00 -1.204426162e+00 -1.204148505e+00 1.2e-04 0.01
7 2.4e-03 4.8e-05 2.2e-07 1.01e+00 -1.201921801e+00 -1.201872363e+00 2.4e-05 0.01
8 2.0e-04 3.9e-06 4.1e-09 1.00e+00 -1.201318320e+00 -1.201316334e+00 2.0e-06 0.01
9 2.3e-05 4.5e-07 1.6e-10 1.00e+00 -1.201275789e+00 -1.201275561e+00 2.3e-07 0.01
10 2.1e-06 4.1e-08 4.3e-12 1.00e+00 -1.201270976e+00 -1.201270959e+00 2.1e-08 0.01
11 2.4e-09 4.9e-11 1.7e-16 1.00e+00 -1.201270465e+00 -1.201270465e+00 2.4e-11 0.01
Optimizer terminated. Time: 0.02
Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: -1.2012704652e+00 nrm: 1e+00 Viol. con: 3e-09 var: 0e+00 cones: 0e+00
Dual. obj: -1.2012704652e+00 nrm: 1e+00 Viol. con: 0e+00 var: 6e-11 cones: 0e+00
Optimizer summary
Optimizer - time: 0.02
Interior-point - iterations : 11 time: 0.01
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +1.20127