% Section 7.1.1
% Boyd & Vandenberghe, "Convex Optimization"
% Kim & Mutapcic, "Logistic regression via geometric programming"
% Written for CVX by Almir Mutapcic 02/08/06
%
% Solves the logistic regression problem re-formulated as a GP.
% The original log regression problem is:
%
%   minimize   sum_i(theta'*x_i) + sum_i( log(1 + exp(-theta'*x_i)) )
%
% where x are explanatory variables and theta are model parameters.
% The equivalent GP is obtained by the following change of variables:
% z_i = exp(theta_i). The log regression problem is then a GP:
%
%   minimize   prod( prod(z_j^x_j) ) * (prod( 1 + prod(z_j^(-x_j)) ))
%
% with variables z and data x (explanatory variables).

randn('state',0);
rand('state',0);

a =  1;
b = -5;

m = 100;
u = 10*rand(m,1);
y = (rand(m,1) < exp(a*u+b)./(1+exp(a*u+b)));

% order the observation data
ind_false = find( y == 0 );
ind_true  = find( y == 1 );

% X is the sorted design matrix
% first have true than false observations followed by the bias term
X = [u(ind_true); u(ind_false)];
X = [X ones(size(u,1),1)];
[m,n] = size(X);
q = length(ind_true);

cvx_begin gp
  % optimization variables
  variables z(n) t(q) s(m)

  minimize( prod(t)*prod(s) )
  subject to
    for k = 1:q
      prod( z.^(X(k,:)') ) <= t(k);
    end

    for k = 1:m
      1 + prod( z.^(-X(k,:)') ) <= s(k);
    end
cvx_end

% retrieve the optimal values and plot the result
theta = log(z);
aml = -theta(1);
bml = -theta(2);

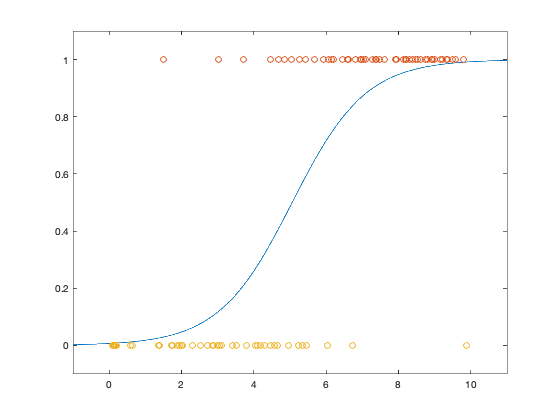
us = linspace(-1,11,1000)';
ps = exp(aml*us + bml)./(1+exp(aml*us+bml));

plot(us,ps,'-', u(ind_true),y(ind_true),'o', ...
                u(ind_false),y(ind_false),'o');
axis([-1, 11,-0.1,1.1]);

 
Calling Mosek 9.1.9: 1320 variables, 401 equality constraints
------------------------------------------------------------

MOSEK Version 9.1.9 (Build date: 2019-11-21 11:32:15)
Copyright (c) MOSEK ApS, Denmark. WWW: mosek.com
Platform: MACOSX/64-X86

Problem
  Name                   :                 
  Objective sense        : min             
  Type                   : CONIC (conic optimization problem)
  Constraints            : 401             
  Cones                  : 200             
  Scalar variables       : 1320            
  Matrix variables       : 0               
  Integer variables      : 0               

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries                  : 2                 time                   : 0.00            
Lin. dep.  - tries                  : 1                 time                   : 0.00            
Lin. dep.  - number                 : 0               
Presolve terminated. Time: 0.00    
Problem
  Name                   :                 
  Objective sense        : min             
  Type                   : CONIC (conic optimization problem)
  Constraints            : 401             
  Cones                  : 200             
  Scalar variables       : 1320            
  Matrix variables       : 0               
  Integer variables      : 0               

Optimizer  - threads                : 8               
Optimizer  - solved problem         : the primal      
Optimizer  - Constraints            : 200
Optimizer  - Cones                  : 201
Optimizer  - Scalar variables       : 603               conic                  : 603             
Optimizer  - Semi-definite variables: 0                 scalarized             : 0               
Factor     - setup time             : 0.00              dense det. time        : 0.00            
Factor     - ML order time          : 0.00              GP order time          : 0.00            
Factor     - nonzeros before factor : 5250              after factor           : 5250            
Factor     - dense dim.             : 0                 flops                  : 3.71e+05        
ITE PFEAS    DFEAS    GFEAS    PRSTATUS   POBJ              DOBJ              MU       TIME  
0   1.6e+00  5.3e+01  2.4e+02  0.00e+00   8.278383991e+01   -1.610204003e+02  1.0e+00  0.00  
1   8.4e-01  2.8e+01  9.8e+01  6.46e-01   6.352338960e+01   -7.701832110e+01  5.3e-01  0.01  
2   8.5e-02  2.9e+00  3.5e+00  7.67e-01   4.063282386e+01   2.473052030e+01   5.4e-02  0.01  
3   5.4e-03  1.8e-01  6.2e-02  9.32e-01   3.334737442e+01   3.230090751e+01   3.4e-03  0.01  
4   3.6e-04  1.2e-02  1.1e-03  9.89e-01   3.300303043e+01   3.293276591e+01   2.3e-04  0.01  
5   2.0e-05  6.7e-04  1.4e-05  9.97e-01   3.298114923e+01   3.297724371e+01   1.3e-05  0.01  
6   1.8e-06  6.0e-05  3.8e-07  9.99e-01   3.297983717e+01   3.297948471e+01   1.1e-06  0.01  
7   2.0e-07  6.6e-06  1.4e-08  1.00e+00   3.297971771e+01   3.297967890e+01   1.3e-07  0.02  
8   2.2e-08  7.0e-07  4.8e-10  1.00e+00   3.297970426e+01   3.297970018e+01   1.3e-08  0.02  
9   2.2e-09  7.1e-08  1.6e-11  1.00e+00   3.297970283e+01   3.297970242e+01   1.3e-09  0.02  
Optimizer terminated. Time: 0.02    


Interior-point solution summary
  Problem status  : PRIMAL_AND_DUAL_FEASIBLE
  Solution status : OPTIMAL
  Primal.  obj: 3.2979702832e+01    nrm: 1e+02    Viol.  con: 3e-09    var: 0e+00    cones: 0e+00  
  Dual.    obj: 3.2979702417e+01    nrm: 1e+00    Viol.  con: 0e+00    var: 7e-08    cones: 0e+00  
Optimizer summary
  Optimizer                 -                        time: 0.02    
    Interior-point          - iterations : 9         time: 0.02    
      Basis identification  -                        time: 0.00    
        Primal              - iterations : 0         time: 0.00    
        Dual                - iterations : 0         time: 0.00    
        Clean primal        - iterations : 0         time: 0.00    
        Clean dual          - iterations : 0         time: 0.00    
    Simplex                 -                        time: 0.00    
      Primal simplex        - iterations : 0         time: 0.00    
      Dual simplex          - iterations : 0         time: 0.00    
    Mixed integer           - relaxations: 0         time: 0.00    

------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +2.10331e+14