% Boyd & Vandenberghe "Convex Optimization"
% Original version by Lieven Vandenberghe
% Adapted for CVX by Michael Grant, 2005/12/19
% Generates figures 7.5-7.8

% The constellation points. Feel free to change them, but they must
% produce a valid Voronoi diagram. Therefore, there must be three or
% more points, and no three can be collinear. To test your selected
% points, run VORONOI( Cs(:,1), Cs(:,2) ) and see if a complete diagram
% is drawn; if so, your points should work.
Cs = [ ...
    0,    0   ; ...
    1.2,  2.4 ; ...
    -3,   +3   ; ...
    -4,    0   ; ...
    -1.6, -3.2 ; ...
    1.84615384615385, -2.76923076923077 ; ...
    2.35294117647059,  0.58823529411765 ];
Cmax = max(max(abs(Cs))) * 1.25;

% Plot the constellation points and the Voronoi tesselation
clf
Cx = Cs( :, 1 );
Cy = Cs( :, 2 );
m  = length( Cx );
Cs = Cs';
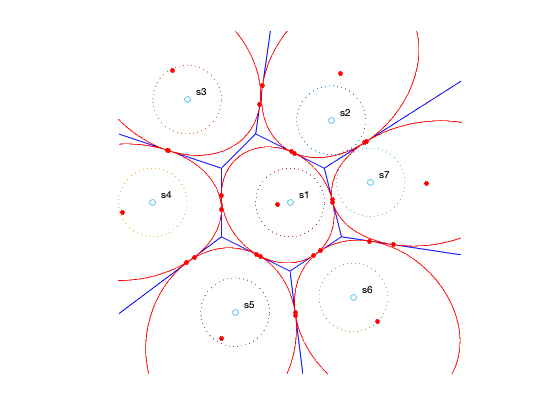
[ Vx, Vy ] = voronoi( Cx, Cy );
plot( Vx, Vy, 'b-', Cx, Cy, 'o' );
axis equal
axis( Cmax * [ -1, 1, -1, 1 ] );
axis off
hold on

% Draw unit circles around each constellation point
noangles = 200;
angles   = linspace( 0, 2 * pi, noangles );
crcpts   = [ cos(angles) ; sin(angles) ];
for i=1 : m,
    text( Cx(i)+0.25, Cy(i)+0.25, [ 's', int2str(i) ] );
    ellipse = [ cos(angles) ; sin(angles) ] + Cs(:,i) * ones(1,noangles);
    plot( ellipse(1,:), ellipse(2,:), ':' );
end;
% print -deps chebbnds_example.eps

% Determine the polyhedrons for each Voronoi region by computing the
% Delaunay triangulation; that is, matrices A and b such that
%     A * ( x - c ) <= b
% where c is the constellation point. The faces of a polyhedron for a given
% point consist of the perpindicular bisectors of edges of the Delaunay
% triangles to which it belongs.
m    = size( Cs, 2 );
tri  = delaunay( Cx, Cy );
ee   = sparse( tri, tri( :, [ 3, 1, 2 ] ), 1, m, m );
ee   = ee + ee';
for k = 1 : m,
    v2 = find( ee( :, k ) );
    pk = Cs( :, v2 );
    qk = Cs( :, k  ) * ones( 1, length( v2 ) );
    Ak = pk - qk;
    bk = 0.5 * sum( Ak .* Ak, 1 );
    As{k} = Ak';
    bs{k} = bk';
end

% For each polyhedron, compute lower bounds on the probability of
% correct detection with sigma = 1. Check the results by plotting the
% ellipsoid x'*P*x + 2*q'*x + r = 1, which should inscribe the polyhedron.
ints = 1 : m;
% Uncomment to do only the first polyhedron, like the book does
% ints = 1;
for i = ints( : ).',
    [ cd_cheb, P, q, r, X, lambda ] = cheb( As{i}, bs{i}, eye(2) );
    ellipse = sqrt(1-r+q'*(P\q)) * P^(-1/2) * crcpts + ...
        (-P\q + Cs(:,i)) * ones(1,noangles);
    plot( ellipse(1,:), ellipse(2,:), 'r-' );
    dots = plot( X(1,:)+Cx(i), X(2,:)+Cy(i), 'ro' );
    set( dots, 'MarkerFaceColor', 'red' );
    set( dots, 'MarkerSize', 4 );
end
hold off
% print -deps chebbnds_example2.eps

% Compute Chebyshev lower bounds for Prob( As(i) * v <= bs(i) )
% where v = N(Cs(i),sigma) for varying values of sigma
nsigma   = 500;
sigmas   = linspace( 0.001, 6.0, nsigma )';
cd_cheb  = zeros( nsigma, m );
fprintf( 'Computing lower bounds' );
% Uncomment to match the book
ints = 1 : m;
% ints     = 1 : 3;
for i = ints( : ).',
    for k = 1 : nsigma,
        cd_cheb(k,i) = cheb( As{i}, bs{i}, sigmas(k) * eye(2) );
    end;
    if rem( k, 10 ) == 0,
        fprintf( '.' );
    end
end;
fprintf( 'done.\n' );

figure(2)
mc = size( cd_cheb, 2 );
plot(sqrt(sigmas(:,ones(1,mc))), cd_cheb);
for i = 1 : mc,
    text( sqrt(sigmas(nsigma/4)), cd_cheb(nsigma/4,i), ['b',int2str(i)] );
end;
xlabel('x');
ylabel('y');
axis( [ 0, 2.5, 0, 1 ] );

% For the central set, compute Chebyshev lower bounds, Monte Carlo
% estimates, and Chernoff bounds.
% for central set, compute cheb lower bounds,  mc estimates,
% and chernoff bounds
%

nsigma = 50;
sigmas = linspace( 0.1, 0.5, nsigma );
cd1    = zeros( 1, nsigma );   % lower bounds for prob( x in C1 )
mc1    = zeros( 1, nsigma );   % monte carlo estimates of prob( x in C1 )
cher1  = zeros( m-1, nsigma ); % chernoff upper bounds on Prob( x in Cj | s = s_1 )
fprintf( 'Computing lower bounds and Monte Carlo sims' );
for i = 1 : nsigma,
    % Compute the Chebyshev lower bound on Prob( As{1} * v <= bs{1} )
    % for v in N( 0, Sigma )
    Sigma  = sigmas(i)^2 * eye(2);
    cd1(i) = cheb( As{1}, bs{1}, Sigma );
    mc1(i) = montecarlo( As{1}, bs{1}, Sigma, 10000 );
    if rem( i, 5 ) == 0,
        fprintf( '.' );
    end
end
fprintf( 'done.\nComputing upper bounds' );
for j = 2 : m,
    A = As{j};
    b = bs{j} - A * ( Cs(:,1) - Cs(:,j) );
    % Compute the Chernoff upper bound on
    %     Prob( As{j} * ( v + Cs{1} - Cs{j} ) <= bs{j} )
    % for v in N( 0, Sigma )
    for i = 1 : nsigma,
        cher1( j - 1, i ) = cher( A, b, sigmas(i)^2*eye(2) );
    end
    fprintf( '.' );
end;
fprintf( 'done.\n' );
cher1 = max( 1 - sum( cher1 ), 0 );
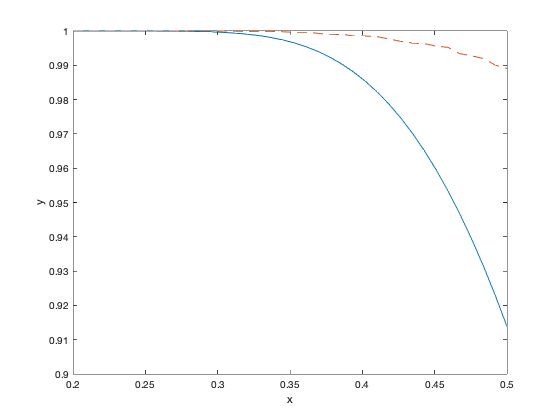
figure(4)
plot( sigmas, cher1, '-', sigmas, mc1, '--' );
axis( [ 0.2 0.5 0.9 1 ] );
xlabel( 'x' );
ylabel( 'y' );
%print -deps chernoff_example.eps

Computing lower bounds.......done.
Computing lower bounds and Monte Carlo sims..........done.
Computing upper bounds......done.