x = [ 0.55 0.0;
0.25 0.35
-0.2 0.2
-0.25 -0.1
-0.0 -0.3
0.4 -0.2 ]';
[n,m] = size(x);
cvx_begin
variable A(n,n) symmetric
variable b(n)
maximize( det_rootn( A ) )
subject to
norms( A * x + b * ones( 1, m ), 2 ) <= 1;
cvx_end
clf
noangles = 200;
angles = linspace( 0, 2 * pi, noangles );
ellipse = A \ [ cos(angles) - b(1) ; sin(angles) - b(2) ];
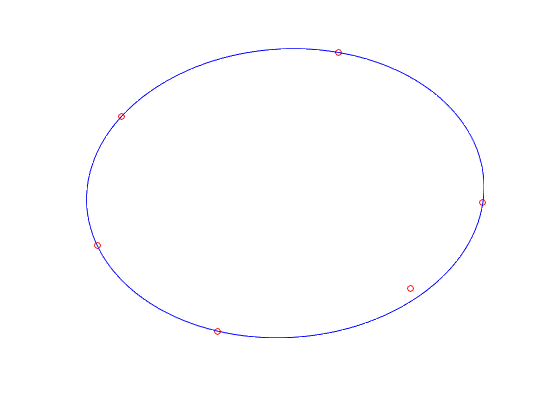
plot( x(1,:), x(2,:), 'ro', ellipse(1,:), ellipse(2,:), 'b-' );
axis off
Calling Mosek 9.1.9: 38 variables, 16 equality constraints
For improved efficiency, Mosek is solving the dual problem.
------------------------------------------------------------
MOSEK Version 9.1.9 (Build date: 2019-11-21 11:32:15)
Copyright (c) MOSEK ApS, Denmark. WWW: mosek.com
Platform: MACOSX/64-X86
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 16
Cones : 7
Scalar variables : 28
Matrix variables : 1
Integer variables : 0
Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 1 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.00
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 16
Cones : 7
Scalar variables : 28
Matrix variables : 1
Integer variables : 0
Optimizer - threads : 8
Optimizer - solved problem : the primal
Optimizer - Constraints : 8
Optimizer - Cones : 7
Optimizer - Scalar variables : 21 conic : 21
Optimizer - Semi-definite variables: 1 scalarized : 10
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 30 after factor : 30
Factor - dense dim. : 0 flops : 6.33e+02
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 1.0e+00 1.0e+00 7.0e+00 0.00e+00 6.000000000e+00 0.000000000e+00 1.0e+00 0.00
1 2.4e-01 2.4e-01 8.1e-01 9.31e-01 1.758136793e+00 3.039930564e-01 2.4e-01 0.01
2 6.1e-02 6.1e-02 2.0e-01 4.69e-01 2.204950365e+00 1.654314776e+00 6.1e-02 0.01
3 1.1e-02 1.1e-02 2.1e-02 5.02e-01 2.674148781e+00 2.557685367e+00 1.1e-02 0.01
4 1.7e-03 1.7e-03 1.2e-03 9.31e-01 2.685852208e+00 2.668281579e+00 1.7e-03 0.01
5 2.0e-04 2.0e-04 4.7e-05 9.92e-01 2.683542756e+00 2.681442137e+00 2.0e-04 0.01
6 1.6e-05 1.6e-05 1.1e-06 9.99e-01 2.683838025e+00 2.683667526e+00 1.6e-05 0.01
7 1.6e-06 1.6e-06 3.4e-08 1.00e+00 2.683972568e+00 2.683955696e+00 1.6e-06 0.01
8 7.3e-08 7.3e-08 3.4e-10 1.00e+00 2.683985203e+00 2.683984423e+00 7.3e-08 0.01
9 4.8e-09 4.9e-09 5.7e-12 1.00e+00 2.683985406e+00 2.683985354e+00 4.8e-09 0.01
Optimizer terminated. Time: 0.02
Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: 2.6839854056e+00 nrm: 1e+00 Viol. con: 2e-08 var: 0e+00 barvar: 0e+00 cones: 0e+00
Dual. obj: 2.6839853543e+00 nrm: 5e+00 Viol. con: 0e+00 var: 4e-13 barvar: 1e-08 cones: 0e+00
Optimizer summary
Optimizer - time: 0.02
Interior-point - iterations : 9 time: 0.01
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +2.68399